INTRODUCTION
Carbon uptake by
secondary forests is a key factor in net emissions calculations for greenhouse
gases. "Carbon uptake" refers
to the net annual per-hectare removal of carbon from the atmosphere while land is
in a given land-use category, such as secondary forest. Uptake is carbon fixed minus carbon released
through respiration and litter decay.
This should not be confused with the net change in carbon that occurs in
converting the original forest to the given land-use category, as by
deforestation. As used here,
"carbon uptake" also does not include the effects of transitions
among land-use categories within the deforested landscape, such as the
emissions from re-clearing secondary forests for agriculture or pasture. Carbon uptake is primarily determined by the
rate of growth of secondary forests of different types. In addition to its importance for global
warming, the rate of growth of secondary forest is also important for assessing
the sustainability of agricultural systems that depend on a fallow period in
woody vegetation in order to regenerate site quality for annual crops or
pasture.
Secondary forests
derived from agriculture (shifting cultivation) grow much faster than do
secondary forests in abandoned cattle pastures.
The rapid growth of shifting cultivation fallows has led Lugo and Brown
(1981, 1982) to present them as greatly mitigating the global warming impact of
deforestation. However, in Brazilian
Amazonia (Figure 1), which is the largest single contributor to the
deforestation component of global greenhouse gas emissions, land-use change is
dominated by cattle pasture rather than by shifting cultivation. In the present paper, data from measurements
of secondary forest growth in abandoned pastures are compared to rates that
other studies have found in shifting cultivation fallows.
(Figure
1 here)
SECONDARY FORESTS
FROM SHIFTING CULTIVATION FALLOWS
The
literature on secondary forest in shifting cultivation fallows throughout the
tropics has been reviewed by Brown and Lugo (1990). These authors plot the existing data for the
dry weights of live biomass in wood, leaves and roots versus the age of the
secondary forest, and trace a freehand curve to represent the growth of each
component. In Table 1, values have been
estimated from Brown and Lugo's (1990) graph for five ages ranging from 5 to 80
years.
(Table 1
here)
Table 1 also
presents three measures that are calculated from the biomass values. The root/shoot ratio decreases from 0.42 in 5-year-old
stands to values around 0.20 after the stands reach age 20 years. The growth rate of total live biomass,
expressed as an average rate since abandonment (mean annual increment),
decreases from about 10 t ha-1 year-1 to 2 t ha-1
year-1 at age 80 years.
Expressed as a growth rate for each interval (periodic annual
increment), the rate is steady at about 10 t ha-1 year-1
until the tenth year, then falls by half by year 20, and continues to decline
to very low levels after year 30.
SECONDARY FORESTS
FROM CATTLE PASTURE
Two
studies of secondary forest derived from abandoned cattle pasture in Brazilian
Amazonia exist: one of the Transamazon Highway colonists in Altamira, Pará
(Guimarães, 1993) and the other in ranches near Paragominas, Pará (Uhl et al.,
1988). In Altamira, measurements were
made in 10 stands of secondary forest with an average age of 4.0 years (range 2
to 7 years) and an average time of use in pasture prior to abandonment of 8.1
years (range 3 to 12 years). The
Paragominas study measured secondary forests in three use-history types: light,
moderate and heavy. Only the moderate
category is considered here; this being the category into which the Altamira
plots would fall and by far the most common pasture-use pattern in Brazilian
Amazonia. The data set from Paragominas
considered here consists of six stands with an average age of 4.6 years (range
1 to 8 years) and an average time under pasture of 8.2 years (range 6 to 12
years).
In the abandoned
pastures in Paragominas studied by Uhl et al. (1988), the growth of
above-ground live biomass of secondary forests in the "moderate" use
category is given by:
Y
= 4.28 A (1)
where:
Y
=above-ground live biomass (t ha-1)
A
=time since abandonment (years)
The average stock of above-ground dead biomass excluding
fine litter is 2.6 t ha-1 and the growth rate (mean annual
increment) is 0.57 t ha-1 year-1 (Table 2). The average fine litter stock is 4.9 t ha-1.
(Table 2
here)
In the abandoned
pastures in Altamira studied by Guimarães (1993), the above-ground biomass
excluding fine litter is given by:
Y =3.38 A - 2.64 B + 35.16 (2)
(P < 0.05, r2=0.80,
N=7)
where:
Y =the
above-ground biomass (live + dead), excluding fine litter.
A
=time since abandonment (years)
B =time used as pasture (years).
The Altamira equation excludes secondary forest stands aged
two or less years. The young stands have
been excluded for several reasons. Since
the age of secondary forest derived from pasture is counted from the date of the
last burn rather than the date the last head of cattle is removed, emissions
from cutting in the first three years are counted as part of pasture
maintenance rather than as secondary forest clearing (Fearnside, in prep.). In addition, because variability of biomass
accumulation is greater in the early years, regressions that include very young
stands explain less of the variance than do those that exclude them. The predicted biomass in the age range of greatest interest (for stands approximately
six years old) is believed to be more reliably predicted by confining the data
to stands nearer this age.
The form of
regression chosen was linear, rather than the exponential form that one might
expect to better represent the slowing of biomass accumulation with time that
characterizes secondary forest growth.
In the Altamira study, linear models explained more of the variance,
regardless of whether young stands were excluded. Since the regression is not being used to
extrapolate far beyond its range, the linear representation is not believed to
result in significant distortion of the predictions.
The calculated
growth rates of secondary forests derived from abandoned pastures are shown in
Table 3 for Paragominas and in Table 4 for Altamira. In the case of Paragominas (Table 3), data
are presented reflecting the mix of pasture use histories studied by Uhl et
al. (1988). In the case of Altamira
(Table 4), the values are derived from Equation 2. Biomass accumulates faster in shifting
cultivation fallows than in the secondary forest derived from pasture at either
site (Figure 2). In Table 5 the
Paragominas data are recalculated to adjust for the difference in mean use
times as pasture in the two data sets (using Equation 2). For the unadjusted data, the stands at
Paragominas grew at a faster rate than those at Altamira at all ages (up to the
maximum of 20 years for the pasture secondary forest data). When adjusted, the Paragominas stands still
grew faster than those at Altamira, except a slightly higher growth rate at
Paragominas during the first (4 to 5 year) interval.
(Tables 3, 4
and 5 here; Figure 2 here)
The calculated
growth rates of the secondary forests in abandoned pastures are compared to
those of shifting cultivation fallows in Table 6. The pattern of slower growth in
pasture-derived secondary forests is maintained. The most important comparison is the biomass
that will be accumulated at the average age at which the secondary forests are
cut. On a regional scale, the average
age at which secondary forest derived from pasture is cut estimated at 6.2
years, while the equivalent value for secondary forest derived from farmland is
5.2 years (Fearnside, 1995). The
weighted average for secondary forests of both origins would be 6.1 years.
Below-ground
biomass estimates are rare. One must
rely on the root/shoot ratio encountered in studies elsewhere, available only
for a few secondary forests in shifting cultivation fallows, rather than
abandoned pastures (see Table 1). The
root/shoot ratio (below-ground biomass/live above-ground biomass) used to
derive approximate below-ground stocks of six-year-old stands is 0.35 (based on
Brown and Lugo, 1990, p. 17).
The average total
biomass expected at age 6.2 years for a pasture-derived secondary forest at
Altamira would be 52.2 t ha-1 (interpolated from Table 4). For a pasture-derived secondary forest at
Paragominas (from Table 5), it would be 51.4 t ha-1 (46.5 t ha-1
total biomass excluding fine litter + 4.9 t ha-1 fine litter), and
for a shifting-cultivation fallow, it would be 66.5 t ha-1:
59.0 t ha-1 total live biomass (interpolated from Table 1) plus
values for dead components equal to those for pasture-derived secondary forests
with moderate use at Paragominas (2.6 t ha-1 dead above-ground excluding
fine litter and 4.9 t ha-1 fine litter). The total biomass of secondary forest derived
from farmland at the average age this category is cut (5.2 years; root/shoot
ratio=0.42) would be 49.6 t ha-1, including the same amounts for
fine litter and other dead above-ground biomass.
(Table 6
here)
CALCULATION OF UPTAKE OF THE REPLACEMENT LANDSCAPE
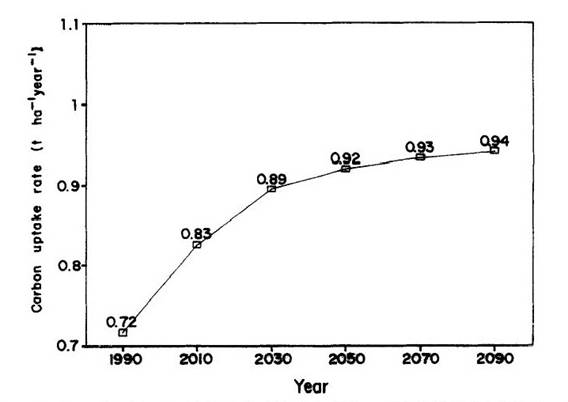
The carbon uptake
rates (t C ha-1 year-1) for land remaining in each of the
land-use categories change over time as shown in Figure 3. If one were to follow the fate of the
landscape that was deforested in a given year, for example 1990, its carbon
stock and and uptake would increase and eventually level off (Figure 4). Note that this is for uptake by an average
hectare in a landscape where secondary forest stands are continually being cut,
thereby repeatedly cycling through the first (most virorously growing) age
classes. The emissions from cutting of
the secondary forest are not included in the uptake figures, such as those in
Figure 4. The carbon uptake rate of
0.97 t ha-1 year-1 after 100 years approximates the
equilibrium condition.
(Figures
3 and 4 here)
The landscape that
replaces forest following deforestation will evolve as the proportions in each
land-use category approach the equilibrium conditions. The fraction of the landscape in each use at
equilibrium can be calculated using a Markov matrix of annual probabilities of
transition among different use categories, if one assumes that farmers and ranchers
in the region do not change their behavior patterns. This has been done using a 98 X 98 matrix
representing six land-use classes with their respective age classes (Fearnside,
1995). At equilibrium, the deforested
landscape has <0.01% regenerated forest (i.e. secondary forest over 100 years
old), 2.6% farmland, 22.8% productive pasture, 36.1% degraded pasture, 2.1%
secondary forest from farmland, and 36.3% secondary forest from pasture.
Carbon uptake will
approach an equilibrium after about 100 years (Figure 5). Carbon uptake can be expected to increase as
the old secondary forests in Pará and Maranhão are cleared and replaced with
younger, more rapidly growing vegetation.
Again, it should be remembered that "carbon uptake" does not
include the release of carbon from cutting the secondary forests.
(Figure
5 here)
The situation in
1990 is summarized in Table 7. The total
(gross) carbon uptake of the landscape is calculated to be 29 X 106
t C year-1 in 1990, or 0.7 t C year-1 ha-1 of
deforested landscape. The uptake for the
landscape in 2090 is calculated to be 365 X 106 t C year-1
(0.9 t C year-1 ha-1 of deforested landscape). This assumes that deforestation continues at
the 11.1 X 103 km2 year-1
1991 rate (Fearnside, 1993) for the 1992-1994 period, after which it increases
at the rates forecast by Reis and Margulis (1991) for the 1995-2030 period, and
remains constant over the 2031-2090 period at the 2030 rate (36 X 103
km2 year-1).
The cumulative deforested area (excluding hydroelectric dams) was 410 X
103 km2 in 1990 (Fearnside, 1993), and would reach 3.9 X
106 km2 in 2090, or virtually the entire forest.
(Table 7
here)
DISCUSSION
It should be
emphasized that substantial uncertainty exists regarding secondary forest growth
rates, especially for the below-ground component. The root/shoot ratio of 0.42 at age four
years used here (based on Brown and Lugo, 1990) is higher than that found in
some studies. Williams-Linera (1983, p.
277) found a root/shoot ratio of 0.21 for a seven-year-old stand in Mexico,
considering roots > 1 mm diameter (regardless of depth) excavated for
individual trees. Szott et al. (1994, p.
185), working in Amazonian Peru, found ratios of 0.15 and 0.09, respectively,
for stands 3.4 and 4.4 years old, implying a ratio of 0.12 at age four years
(considering only roots to 45-cm depth, extracted from soil monoliths by
washing on a 1-mm sieve). Were a lower
root/shoot ratio used in the calculation, carbon uptake would be less than the
amounts estimated in the present paper.
Carbon uptake by
the replacement vegetation is an important part of the carbon balance in areas
undergoing tropical deforestation.
Uptake has often been omitted from global warming calculations for lack
of data. On the other hand, exaggerated
expectations have sometimes been expressed with respect to this uptake in
Brazil, some even suggesting that the sink in secondary forest growth could be
completely counteracting the emissions from deforestation in the region. Unfortunately, the landscape could not
possibly be taking up the amount of carbon that this notion implies, even if a
variety of optimistic assumptions are made.
Suggestions that
all carbon emissions from Brazilian deforestation might be being offset by
uptake from the replacement vegetation are based on one or more of the
following erroneous assumptions: 1) that
young (post-1970) secondary forests cover either all or a much larger fraction
of the replacement landscape than is the case, 2) that no emissions occur from
clearing of secondary forests, and/or 3) that no emissions occur from reburning
and decay of original forest biomass not consumed in the initial burn. Two additional factors have often contributed
to exaggeration of uptake related to deforestation emissions: 1) assumption
that secondary forests are shifting cultivation fallows rather than abandoned
cattle pastures, and 2) use of deforestation emission estimates based on forest
biomass that significantly underestimates the carbon stock, and hence emissions
(see review of biomass estimates in Fearnside et al., 1993).
A major reason
that the deforested terrestrial landscape takes up so much less carbon than
might be imagined is that only 31% of the deforested area is in young
(post-1970) secondary forest, and, of this, 90% is abandoned pasture rather
than agricultural fallows (Table 7). The
uptake by the replacement vegetation is almost completely offset by emissions
from secondary forest clearing within the replacement landscape. In addition, in order to negate the effects
of deforestation, net uptake of the replacement landscape would have to be
greater than the total emission including oxidation of unburned forest remains,
either through decay or through combustion when pastures and fallows are
reburned in succeeding years. Carbon
release from original forest biomass not consumed in the initial burn roughly
triples the gross emissions from deforestation as compared to the initial
combustion releases alone.
Considering carbon
dioxide carbon only, the annual balance of emissions in 1990 (excluding
hydroelectric dams and logging) included gross emissions of 62.2 X 106
t C year-1 from the initial burn, 261.5 X 106 t C year-1
from decay and reburnings of original forest biomass; 27.4 X 106 t C
from burning and decay of secondary forest biomass (including pre-1970
secondary forests); 31.5 X 106 t C from the top 20 cm of soil, and
zero net emission from pasture biomass (which re-absorbs emitted carbon through
annual regrowth), or a total of 382.6 X 106 t C year-1 in
the form of CO2. The uptake
of 29.4 X 106 t C year-1 calculated here corresponds to
only about 8% of these emissions, (considered here on a carbon-only basis: the
percentage would be less if considered in terms of CO2-equivalent
carbon) (Fearnside, in prep.). The 1990
uptake of 29.4 X 106 t C year-1 is only 2.0 X 106
t C greater than the 27.4 t C year-1 estimated emission in that year
from clearing secondary forest (including 5 X 106 t C from
"old", or pre-1970, secondary forests), indicating that the net flux
from the replacement landscape offset a minuscule 0.5% of the deforestation
emissions.
CONCLUSIONS
Land-use change in
Brazilian Amazonia is dominated by transformation of forest to cattle
pasture. Degraded cattle pastures
regenerate secondary forests more slowly than do fallows in shifting
cultivation, leading to lower uptake of carbon than is sometimes believed. The 1990 rate of emissions from deforestation
and secondary forest clearing in the region greatly exceeds the uptake from
regrowth of replacement vegetation. The
calculations presented here indicate that in 1990 the landscape was taking up
29 X 106 t of carbon and emitting 27 X 106 t C annually,
or a net removal of only about 0.5% of the gross emissions in that year. Were the present land-use change processes to
continue with the deforestation rate increasing in accord with a forecast,
uptake by 2090 would increase to 365 X 106 t C year-1, or
about one-third of annual gross emissions, at which time the deforested area
would be about 10 times the 1990 one, and the annual deforestation rate, under
the assumptions of the forecast, about triple the 1990 rate (note that the
cumulative area cleared by 2090 corresponds approximately to the whole of the
forest, after which there could be no further deforestation). Land-use change in Brazilian Amazonia would
continue to result in net releases of large quantities of carbon even with the
large areas of secondary vegetation expected to replace primary forest over the
next century.
ACKNOWLEDGMENTS
The study was
funded by the Pew Scholars Program in Conservation and the Environment and by
the 'Capacidade de Suporte Humano na Amazônia' project of the Fundação Banco do
Brasil (FBB) (No. 10/1615-2). S.V.
Wilson and two anonymous reviewers made helpful comments
REFERENCES
Bartholomew, W.V., Meyer, J. and Laudelout, H., 1953.
Mineral nutrient immobilization under forest and grass fallow in the Yangambi
(Belgian Congo) region. Publication
de l'Institut Nacional pour l'étude Agronomique du Congo Belge. Série
Scientifique No. 57, 27 pp.
Brown, S. and Lugo, A.E., 1990. Tropical secondary forests.
J. Trop. Ecol., 6: 1-32.
Ewel, J.J., 1971. Biomass changes in early tropical
succession. Turrialba, 21: 110-112.
Ewel, J.J., 1975. Biomass of second growth tropical moist
forest. In: F.B. Golley, J.T. McGinnis, R.G. Clements, G.I. Child and M.J.
Duever (Editors), Mineral Cycling in a Tropical Moist Forest Ecosystem. Univ.
of Georgia Press, Athens, pp. 143-150.
Fearnside, P.M., 1993. Deforestation in Brazilian Amazonia:
The effect of population and land tenure. Ambio, 22(8):
537-545.
Fearnside, P.M., 1995. Amazonian deforestation and global
warming: Carbon stocks in vegetation replacing Brazil's Amazon forest. For.
Ecol. Manage. [forthcoming].
Fearnside, P.M., In prep. Amazonia and global warming:
Annual balance of greenhouse gas emissions from land-use change in Brazil's
Amazon region. Paper presented at the
American Geophysical Union Chapman Conference on Biomass Burning and Global
Change, March 13-17, 1995, Williamsburg, Virginia (forthcoming).
Fearnside, P.M., Leal Filho, N. and Fernandes, P.M., 1993.
Rainforest burning and the global carbon budget: Biomass, combustion efficiency
and charcoal formation in the Brazilian Amazon. J. Geophys. Res., 98(D9): 16,733-16,743.
Guimarães,
W.M., 1993. Liberação de carbono e mudanças nos estoques dos nutrientes
contidos na biomassa aérea e no solo resultante de queimadas de florestas
secundárias em áreas de pastagens abandonadas, em Altamira, Pará. Masters
Thesis, Instituto Nacional de Pesquisas da Amazônia/Fundação Universidade do
Amazonas (INPA/FUA), Manaus, AM, 69 pp.
Lugo, A.E. and Brown, S., 1981. Tropical lands: Popular
misconceptions. Mazingira, 5(2): 10‑19.
Lugo, A.E. and Brown, S., 1982. Conversion of tropical moist
forests: A critique. Interciencia, 7(2): 89‑93.
Reis, E.J. and Margulis, S., 1991. Perspectivas Econômicas do Desflorestamento da
Amazônia. Textos para Discussão No. 215. Instituto de Pesquisa Econômica
Aplicada (IPEA), Brasília, DF, 47 pp.
Saldarriaga, J.G., West, D.C. and Tharp, M.L., 1986. Forest
Succession in the Upper Rio Negro of Colombia and Venezuela. Oak Ridge National
Laboratory, Environmental Sciences Publication No. 2694, ORNL/TM-9712. National
Technical Information Service, Springfield, VA, 164 pp.
Szott, L.T., Palm, C.A. and Davey, C.B., 1994. Biomass and
litter accumulation under managed and natural tropical fallows. For. Ecol.
Manage., 67: 177-190.
Uhl, C., Buschbacher, R. and Serrão, E.A.S., 1988. Abandoned
pastures in Eastern Amazonia. I. Patterns of plant succession. J. Ecol., 76:
663-681.
Williams-Linera, G., 1983. Biomass and nutrient content of
two successional stages of tropical wet forest in Uxpanda, Mexico. Biotropica,
15(4): 275-284.
Figure legends
Figure 1:Brazil's Legal Amazon region. Of this 5 X 106 km2
administrative region (60% of Brazil), 4 X 106 km2 was
originally forested.
Figure 2:Biomass accumulation per hectare in
shifting cultivation and pasture.
Figure 3:Carbon uptake per different by different
land uses.
Figure 4:Projected annual carbon uptake per
hectare for land deforested in 1990.
Note that stands in this landscape are continually being cut and
returned to the younger (more vigorously growing) categories, and that the
emissions from the cutting of secondary forests are not included in the uptake
rates of the landscape.
Figure 5:Projected annual carbon uptake per
hectare for the landscape in deforested areas (410 X 103 km2
in 1990, increasing to 3.9 X 106 km2 in 2090).
TABLE
1: SHIFTING CULTIVATION FALLOW GROWTH(a)
Age Live biomass (t ha-1) Root/ Average Growth
(years) ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ shoot growth rate of
Wood Leaves Roots Total ratio rate
of total live
live total live biomass
biomass in
since interval
abandon‑ (t ha-1
ment year-1)(c)
(t ha-1
year-1)(b)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑
5 29.2 4.0 13.8 47.0 0.42 9.4 9.4
10 70.8 6.0 23.1 99.9 0.30 10.0 10.6
20 110.8 10.0 24.2 145.0 0.20 7.3 4.5
30 113.8 9.5 27.7 151.0 0.22 5.0 0.6
80 135.4 8.0 28.5 171.9 0.20 2.1 0.4
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑
(a)
Biomass values estimated from graph drawn by Brown and Lugo (1990, p. 17) based
on data from on Bartholomew et al. (1953), Ewel (1971, 1975), Saldarriaga et
al. (1986) and Williams‑Linera (1983).
(b)
Mean annual increment.
(c)
Periodic annual increment.
TABLE
2: SECONDARY FOREST GROWTH RATES IN
ABANDONED PASTURES
LOCATION Pasture Fre- Growth rate (t ha-1 year-1)
type quency ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------
(%
of Above- Above-
pastures) ground ground
live total
biomass excluding
fine
litter
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑------
Paragominas Light 20 10.72 11.84
use
Moderate 70 4.28 4.84
use
Heavy 10 2.13 2.27
use
Weighted 5.35 5.99
average
Altamira Moderate 100 6.5
use
-------------------------------------------------------------
Stand ages Use
periods
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ (years since (years
as pasture)
Above- Approx- abandonment)
ground imate
total total ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑------------
(above- Mean Range Mean Range
+ below-
ground)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑---------------
21.23 21.23 6.0 3.5-8 1.0 0-4
5.92 5.92 4.6 1-8 8.2 6-12
3.85 3.85 3.9 2.588 8.7 8-11
8.77 8.77 4.8 6.8
4 2-7 8.1 3-12
--------------------------------------------------------------
Sample Description
of pasture type Source
size
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑
4 Seeded to pasture but never weeded. Uhl et al., 1988
Abandoned
shortly after pasture formation.
Grazing
intensity <0.5 adult animals ha-1.
6 Weedings and burnings every 1-3 Uhl et al., 1988
years. Abandoned after 6-12 years.
Grazing
intensity 0.5-1.5 adult animals ha-1.
3 After several weedings and burnings, Uhl et al., 1988
vegetation
bulldozed into windrows and
burned;
pasture replanted and abandoned
6-13
years later. Grazing intensity
0.5=1.5
adult animals ha-1.
10 Guimarães,
1993
-----------------------------------------------------------------
TABLE 3:
CALCULATED BIOMASS AND GROWTH RATES IN ABANDONED PASTURES (Paragominas)
Time Expected Expected Expected Root/
since above- above- above- shoot
abandon- ground ground ground ratio
ment live biomass biomass
(years) biomass excluding including
(t
ha-1) fine fine
litter litter
(t
ha-1) (t ha-1)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑----------
4.8 25.7 28.7 42.1 0.42
5.0 26.8 29.9 43.9 0.42
8.0 42.8 47.9 70.2 0.35
10.0 53.5 59.9 87.7 0.30
15.0 80.3 89.8 131.6 0.25
20.0 107.0 119.7 175.5 0.20
------------------------------------------------------
(a) Mean annual
increment.
(b) Periodic annual
increment.
TABLE 4: CALCULATED BIOMASS AND GROWTH RATES IN
ABANDONED PASTURES (Altamira)
Time Expected Expected Expected Root/
since above- above- above- shoot
abandon- ground ground ground ratio
ment live biomass biomass
(years) biomass excluding including
(t ha-1)(a) fine fine
litter litter
(t ha-1) (t ha-1)(a)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------
4.0 25.0 27.3 32.2 0.42
5.0 27.8 30.7 35.6 0.42
8.0 36.3 40.8 45.7 0.35
10.0 41.9 47.5 52.5 0.30
15.0 55.9 64.4 69.4 0.25
20.0 70.0 81.3 86.2 0.20
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------
(a)
Assumes same dead biomass accumulation rate and fine litter stock as found by
Uhl et al. (1988) in moderate use pasture in Paragominas.
(b)
Mean annual increment.
(c)
Periodic annual increment.
Approx- Total Total Above- Above-
imate biomass biomass ground ground
total growth growth biomass biomass
biomass rate rate growth growth
(t ha-1) since in rate rate
abandon- interval since in
ment (t ha-1
abandonment interval
(t ha-1 year-1) (t ha-1 (t ha-1
year-1) year-1)(b) year-1)(c)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------
38.6 9.7 9.7 6.8 6.8
43.4 8.7 4.8 6.1 3.4
54.9 6.9 3.8 5.1 3.4
61.8 6.2 3.5 4.8 3.4
80.6 5.4 3.7 4.3 3.4
97.6 4.9 3.4 4.1 3.4
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------
TABLE
5: CALCULATED BIOMASS AND GROWTH RATES
IN ABANDONED PASTURES IN PARAGOMINAS COMPARABLE TO ALTAMIRA PASTURES
Time Expected Expected Expected Root/
since above- above- above- shoot
abandon- ground ground ground ratio
ment live biomass biomass
(years) biomass excluding including
(t
ha-1) fine fine
litter litter
(t
ha-1) (t ha-1)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------------
4.0 17.1 19.4 24.3 0.42
5.0 21.4 24.2 29.2 0.42
8.0 34.2 38.7 43.7 0.35
10.0 42.8 48.4 53.4 0.30
15.0 64.2 72.7 77.6 0.25
20.0 85.6 96.9 101.8 0.20
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑--------------------
Note: Moderate-use pasture only, average age since
abandonment 4.0 years (considering all Altamira plots). Altamira pastures average use as pasture =
8.1 years.
Approx‑ Total Total
imate biomass biomass
total growth growth
rate
biomass rate in
interval
excluding since excluding
fine abandon- fine
litter ment litter
(t ha-1) (t ha-1 year-1) (t ha-1 year-1)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑--------------
26.5 6.6 6.6
33.1 6.6 6.6
50.6 6.3 5.8
61.3 6.1 5.3
88.7 5.9 5.5
114.0 5.7 5.1
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑----------------
TABLE 6: COMPARISON OF CALCULATED GROWTH OF SECONDARY
FOREST IN ABANDONED PASTURE AND IN SHIFTING CULTIVATION FALLOWS
Age Total
live biomass
(years) (t
ha-1)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑----
Shifting Abandoned Abandoned
culti- pasture pasture
vation(a) (Alta- (Parago-
mira) minas)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
5 47.0 38.6 55.0
10 99.9 61.8 72.3
20 145.0 97.6 111.2
30 151.0
80 171.9
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------------------
(a) Shifting cultivation
values calculated from Brown and Lugo (1990); abandoned pasture values from
Altamira from Guimarães (1993) and from Paragominas from Uhl et al. (1988). See Tables 3 and 5.
(b) Mean annual increment.
(c) Periodic annual increment.
Average total live biomass growth
since abandonment
(t ha-1 year-1)(b)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑----------
Shifting Abandoned Abandoned
culti- pasture pasture
vation (Alta- (Parago-
mira) minas)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑----------
9.4 8.7 6.6
10.0 6.2 6.1
7.3 4.9 5.7
5.0
2.1
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑----------
Average total live biomass growth
in interval
(t ha-1 year-1)(c)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
Shifting Abandoned Abandoned
culti- pasture pasture
vation (Alta=- (Parago-
mira) minas)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
9.4 8.7 6.6
10.6 3.7 3.5
4.5 3.6 3.9
0.86
0.4
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
TABLE 7: CARBON UPTAKE SUMMARY FOR 1990
Vegetation Area Percent Average
type present of age
of
(103
ha) defor- land
ested use
area (years)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
Farmland 2,221 5 1
Productive 18,400 45 4
pasture
Degraded 904 2.2 4
pasture
Secondary 854 2 3
forest
from farmland
Secondary 11,536 28 3
forest
from pasture
Pre-1970 7,127 17 30
secondary forest
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
Total: 41,042 100.0 8
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-----
Total Average Average Total Average
biomass total carbon carbon carbon
(106
t) biomass content stock stock
(t ha-1) (%)
(106 t) (t ha-1)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑---------------
1 1
45 1 0
196 11
45 88 5
3 3.4
45 1
1.5
25 29
45 11 13
508 44
45 229 20
1,053 148
45 474
67
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑---------------
1,787 43.5
45 804
19.6
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑---------------
Average Total Average Total
growth growth carbon carbon
rate (t (106
t uptake (t uptake
ha-1 year-1) year-1) C ha-1 year-1) (106 t)
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑-------------------
0 0 0 0
0 0 0 0
0.8 1 0.4 0
10 8 4 4
5 54 2 24
0 2 0 1
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑--------------
1.6 65 0.7 29
‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑--------------
Fig. 1
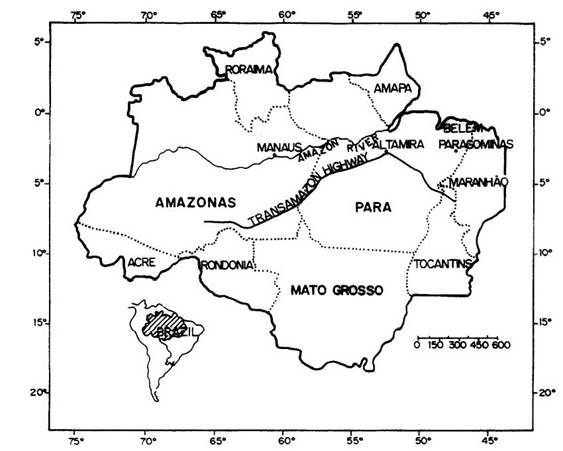
Fig. 2
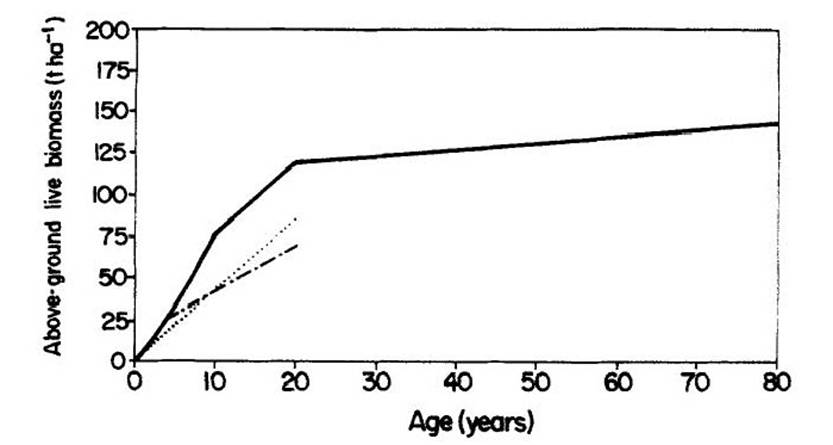
Fig. 3
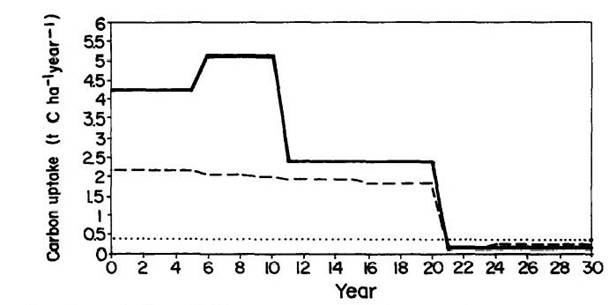
Fig. 4
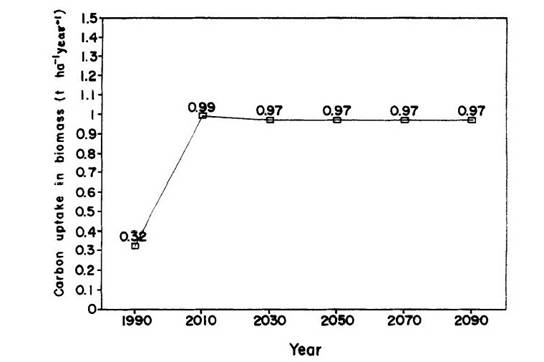
Fig. 5