






Hidrelétricas Planejadas no
Rio Xingu como Fontes de Gases do Efeito Estufa: Belo Monte (Kararaô) e
Altamira (Babaquara)
Philip M.
Fearnside
Coordenação
de Pesquisas em Ecologia-CPEC
Instituto
Nacional de Pesquisas da Amazônia-INPA
Av.
André Araújo, 2936
C.P.
478
69011-970
Manaus-Amazonas
Contribuição para:
O. Seva & G. Switkes (eds.) As
Questões Energéticas, Ambientais e Políticas na Tentativa de Construção das
Hidrelétricas no Rio Xingu, Brasil: Os projetos Belo Monte (Kararaô) e Altamira
(Babaquara), Pará. Coalição Rios Vivos, São Paulo. 344 p. (2005)
15 de dez. de 2004
20 de dez. de 2004
20 de jan. de 2005
pequenas correções: 29 de jan. de 2005
revisão de português:
10 de fev. de 2005
RESUMO
Calcular
as emissões de gases de efeito estufa de barragens hidrelétricas é importante
no processo de tomada de decisão em investimentos públicos nas várias opções
para geração e conservação de energia elétrica. A proposta da hidrelétrica de
Belo Monte (antigamente Kararaô) e sua contrapartida rio acima, a hidrelétrica
de Altamira (mais conhecida por seu nome anterior: Babaquara), está no centro das
controvérsias sobre como deveriam ser calculadas as emissões de gases de efeito
estufa de represas. A hidrelétrica de Belo Monte por si só teria uma área de
reservatório pequena (440 km2) e capacidade instalada grande
(11.181,3 MW), mas a represa de Babaquara que regularizaria a vazão do rio
Xingu (aumentando assim a geração de energia de Belo Monte) inundaria uma vasta
área (6.140 km2). Está previsto que, em cada ano, o nível d’água em
Babaquara vai variar em 23 m, expondo assim repetidamente uma área de 3.580 km2
(a zona de deplecionamento) a uma vegetação herbácea, de fácil decomposição, que
cresceria rapidamente. Esta vegetação se decomporia a cada ano no fundo do
reservatório quando o nível d’água sobe, produzindo metano. O metano oriundo da
vegetação da zona de deplecionamento representa uma fonte permanente deste gás
de efeito estufa, diferente do grande pulso de emissão oriunda da decomposição
dos estoques iniciais de carbono no solo e nas folhas e liteira (serapilheira
ou foliço) da floresta original. As turbinas e vertedouros puxam água de níveis
abaixo do termoclino, isto é, da barreira de estratificação por temperatura que
isola a água do fundo do reservatório, rica em metano, da camada superficial
que está em contato com o ar. Quando a água do fundo emerge das turbinas e dos
vertedouros, grande parte da sua carga de metano dissolvido é liberado para a
atmosfera. O gás carbônico oriundo da decomposição da parte superior das
árvores da floresta inundada, que fica acima d’água, representa outra fonte
significativa de emissão de gás de efeito estufa nos primeiros anos depois da
formação de um reservatório.
Belo
Monte e Babaquara representam um desafio ao ainda principiante sistema
brasileiro de avaliação de impacto ambiental e licenciamento de obras. O
procedimento atual considera cada projeto de infra-estrutura isoladamente, em
lugar de avaliar a gama completa de impactos que o conjunto como um todo
provocaria. Neste caso, as características excepcionalmente favoráveis da
primeira barragem (Belo Monte) são altamente enganadoras como indicações das
conseqüências ambientais de uma decisão para construir aquela obra. Os impactos principais serão provocados pelos
reservatórios muito maiores rio acima, começando pelo de Babaquara e,
possivelmente, outras quatro represas planejadas na bacia do Xingu, que
inundariam grandes áreas de floresta tropical e terra indígena, além de emitir
gases de efeito estufa. A presente análise indica que o complexo Belo
Monte/Babaquara não teria um saldo positivo, em termos de emissões de gases de
efeito estufa, comparado ao gás natural, até 41 anos após o enchimento da
primeira represa. Isto, na forma de
cálculo mais favorável para hidrelétricas, com zero de desconto para os
impactos no aquecimento global, essencialmente como se o impacto pesado nos
primeiros anos fosse um empréstimo sem juros.
A aplicação de qualquer taxa de desconto acima de 1,5% ao ano resulta no
complexo não ter um saldo positivo, comparado ao gás natural, até o final do
horizonte de tempo de 50 anos usado no Brasil em avaliações de projetos
propostos de energia. O impacto sobre o aquecimento global de represas é uma
indicação da necessidade de o País reavaliar as suas políticas atuais, que
alocam grandes quantias de energia da rede nacional para uma indústria subsidiada
de exportação de alumínio.
I.
O Rio Xingu e as Barragens mais Controversas da Amazônia
A proposta da hidrelétrica de Belo
Monte, no rio Xingu (um afluente do rio Amazonas no Estado do Pará), é o foco
de intensa controvérsia devido à magnitude e à natureza dos seus impactos. A
hidrelétrica de Belo Monte ficou conhecida pela ameaça que representa aos povos
indígenas por facilitar uma série de represas planejadas rio acima em áreas
indígenas. O impacto de Belo Monte sobre o efeito estufa provém das represas
rio acima, projetadas para aumentar substancialmente a produção elétrica de
Belo Monte e para regularizar a vazão do rio Xingu, altamente sazonal. O
reservatório de Belo Monte é pequeno relativamente à capacidade de suas duas
casas de força, mas os cinco reservatórios rio acima seriam grandes, até mesmo
pelos padrões amazônicos. O maior desses reservatórios é a represa de
Babaquara, recentemente renomeada de “Altamira”, num esforço aparentemente com o
propósito de escapar do ônus da crítica que os planos para Babaquara atraíram
ao longo das últimas duas décadas (o inventário inicial para a obra começou em
outubro de 1975).
“Barrageiros” ou construtores de
barragens representam uma subcultura distinta na sociedade brasileira (veja
Fearnside, 1989, 1990). A barragem de Belo Monte tem um lugar especial na
cultura dos barrageiros. Um dos engenheiros envolvidos no planejamento da
barragem explicou a natureza especial da obra assim: “Deus só faz um lugar como
Belo Monte de vez em quando. Este lugar foi feito para uma barragem”. Com 87,5
m de queda e uma vazão média de 7.851 m3/segundo (média no período de
1931 a 2000), outro local como Belo Monte é difícil de se encontrar. Apesar da
variação sazonal alta no fluxo d’água, que diminui o potencial de energia que o
local (por si só) pode oferece, a questão principal levantada pela hidrelétrica
de Belo Monte é mais profunda que os impactos diretos no local do reservatório:
é o sistema pelo qual as decisões sobre construção de barragens acontecem. Em
um Brasil ideal, Belo Monte poderia produzir, pelo menos em grande parte, os
benefícios que seus promotores retratam. Mas no Brasil real de hoje, em lugar
disso, a obra levaria a impactos sociais e ambientais desastrosos em troca do
pouco benefício para a população brasileira. A existência de Belo Monte
forneceria a justificativa técnica para a construção de represas rio acima que
inundariam vastas áreas de terra indígena, praticamente todas sob floresta
tropical, em troca de subsidiar os lucros de companhias de alumínio
multinacionais que empregam pouca mão-de-obra no Brasil (veja outros capítulos
neste volume).
A hidrelétrica de Belo Monte propriamente dita é apenas
a “ponta do iceberg” do impacto do projeto. O impacto principal vem da cadeia de
represas rio acima, presumindo que o embalo político começado pela Belo Monte aniquilasse
o sistema de licenciamento ambiental, ainda frágil, do Brasil. Este é o quadro provável
da situação para a maioria dos observadores não ligados à indústria
hidrelétrica. Das represas rio acima, o reservatório de Babaquara, com duas
vezes a área inundada da barragem de Balbina, seria o primeiro a ser criado.
Autoridades do setor elétrico se esforçam para separar o projeto Belo Monte
propriamente dito do seu impacto principal, que é o de incentivar as
megabarragens planejadas a montante.
Embora
estudos iniciais, completados em 1989, tenham analisado o projeto para Belo
Monte com inclusão dos benefícios da regularização da vazão por represas rio
acima, a dificuldade em obter uma aprovação rápida logo ficou patente às
autoridades do setor elétrico. A exigência de um estudo de impacto ambiental
(EIA) no Brasil entrou em vigor em janeiro de 1986, e a constituição federal de
outubro de 1988 estipulou a exigência de aprovação pelo Congresso Nacional para
projetos que inundam áreas indígenas. Um estudo novo foi elaborado, então, para
Belo Monte sem a presunção da regularização da vazão por represas a montante. O
estudo revisado (atual) afirma:
O estudo energético em
questão considera apenas a existência do Complexo Hidrelétrico Belo Monte no
rio Xingu, o que acarreta que o mesmo não aufira qualquer benefício de regularização
a montante. Embora os estudos de inventário hidrelétrico do rio Xingu
realizados no final da década de 70 tivessem identificado 5 aproveitamentos
hidrelétricos a montante de Belo Monte, optou-se por não considerá-los nas
avaliações aqui desenvolvidas, em virtude da necessidade de reavaliação deste
inventário sob uma nova ótica econômica e sócio-ambiental. Frisa-se, porém, que
a implantação de qualquer empreendimento hidrelétrico com reservatório de
regularização a montante de Belo Monte aumentará o conteúdo energético dessa
usina.
(Brasil,
ELETRONORTE. s/d [C. 2002]a, p. 6-82).
Em outras palavras, embora uma decisão política tenha
sido tomada para restringir a análise oficial somente à Belo Monte como uma
conveniência necessária para obter a aprovação do projeto, as vantagens
técnicas de construir também as represas rio acima (especialmente Babaquara)
permanecem as mesmas. Na realidade, nem a ELETRONORTE nem qualquer outra
autoridade governamental prometeram deixar de construir essas barragens, mas
apenas adiar uma decisão sobre elas. Este é o ponto crucial do problema.
Todo
mundo já ouviu o provérbio do “camelo-na-barraca”: um beduíno acampado no
deserto pode ser tentado a deixar o seu camelo pôr a cabeça dentro da barraca, à
noite, para se proteger de uma tempestade de areia. Mas ao acordar na manhã
seguinte, com certeza o homem encontrará o camelo de corpo inteiro dentro da
barraca. Esta é exatamente a situação com Belo Monte: uma vez que a Belo Monte
comece, nós, provavelmente, vamos acordar e encontrar Babaquara já instalada.
O
enredo do “camelo-na-barraca” já aconteceu com projetos da ELETRONORTE em pelo
menos duas ocasiões paralelas. A primeira ocorreu durante o enchimento do
reservatório de Balbina. Em setembro de 1987, menos de um mês antes do começo
do enchimento do reservatório, a ELETRONORTE emitiu um “esclarecimento público”
declarando que o reservatório seria enchido somente até a cota de 46 m sobre o
nível médio do mar (abaixo do nível originalmente planejado de 50 m). Uma série
de estudos ambientais seria realizada durante vários anos para monitorar a
qualidade da água antes de tomar uma decisão separada sobre o enchimento do
reservatório até a cota de 50 m (Brasil, ELETRONORTE, 1987a). Porém, quando o
nível d’água alcançou a cota de 46 m, o processo de enchimento não parou
durante um único segundo para os estudos ambientais planejados, e o enchimento
continuou sem interrupção até a cota de 50 m e até mesmo além deste nível (veja
Fearnside, 1989, 1990). Na realidade, o plano em vigor durante todo o processo
de encher a represa indicava enchimento direto até o nível de 50 m (Brasil,
ELETRONORTE, 1987b). Hoje a represa é
operada, sem nenhuma justificativa, com um nível máximo operacional de 51 m.
O
segundo exemplo é a expansão em 4.000 W da capacidade instalada em Tucuruí (i.e., Tucuruí-II). Um estudo de impacto
ambiental estava sendo elaborado para o projeto de Tucuruí-II, já que a
constituição brasileira de 1988 exige um EIA para qualquer hidrelétrica com 10
MW ou mais de capacidade instalada.
Porém, o EIA foi truncado quando a ELETRONORTE começou a construir o
projeto sem um estudo ambiental em 1998 (veja Fearnside, 2001). O raciocínio
era que a obra não teria nenhum impacto ambiental porque o nível máximo
operacional normal da água no reservatório permaneceria inalterado em 72 m
sobre o nível médio do mar (Indriunas, 1998). No entanto, enquanto a construção
estava em andamento, a decisão foi mudada discretamente para elevar o nível
d’água até 74 m, como era o plano original.
A represa está sendo operada neste nível desde 2002, também sem justificativa.
Essa estratégia também é percebida
para Belo Monte. O estudo de viabilidade admite que
“...os serviços de infra-estrutura (acessos, canteiros, sistema de transmissão, vila residencial, alojamentos) terão início tão logo a sua licença de instalação seja aprovada, o que deve ocorrer separadamente da aprovação da licença para as obras civis principais, no decorrer do denominado ano “zero” de obra.” (Brasil, ELETRONORTE, 2002, Tomo II, p. 8-155).
Isto significa que
o estudo ambiental e o processo de licenciamento para a barragem de Belo Monte
são vistos como uma mera formalidade burocrática para legalizar uma decisão que
já foi tomada. Se o licenciamento ambiental fosse visto como uma contribuição
essencial à própria decisão sobre se o projeto deveria ou não ir adiante, então
não haveria razão para começar o trabalho de infra-estrutura complementar
enquanto o projeto principal (a barragem) continua sob consideração.
Estes
exemplos são indicações pouco favoráveis para o futuro do Xingu. Eles sugerem
que, embora as autoridades possam dizer agora o que bem quiserem sobre planos
para Belo Monte operar com uma única barragem, quando, no decorrer do tempo chegar
a hora para começar o trabalho na segunda barragem (Babaquara), é provável que
a obra vá adiante de qualquer maneira.
Isto significa que os impactos de represas a montante devem ser
considerados, e, se estes impactos forem julgados inaceitáveis, então qualquer
decisão para construir Belo Monte deve ser acompanhada de um mecanismo
confiável para garantir que as barragens rio acima não serão construídas.
Se a
Belo Monte é realmente economicamente viável sem Babaquara, como afirma a
ELETRONORTE, isto não diminuiria o perigo da história se desdobrar para
produzir os desastres ambientais e sociais implícitos no esquema de Babaquara.
Isto porque, depois da conclusão de Belo Monte, o processo de tomada de decisão
sobre a construção de Babaquara seria dominado por argumentos de que a
Babaquara seria altamente lucrativa como meio de aumentar o potencial elétrico
de Belo Monte.
Porém, a Belo Monte poderia conduzir
a um resultado diferente. Antes de se decidir sobre a construção de Belo Monte,
o sistema de tomada de decisão sobre barragens hidrelétricas deve ser mudado radicalmente.
Devem ser enfrentadas as perguntas básicas sobre o que é feito com a energia,
assim como também a questão de quanta energia realmente é necessária. O governo
brasileiro deveria deixar de encorajar a expansão de indústrias intensivas de
energia. Além disso, estas indústrias,
especialmente a de alumínio, deveriam ser fortemente penalizadas, cobrando-as
pelo dano ambiental que o uso intensivo de energia implica. Ademais, o governo
brasileiro precisa desenvolver uma base institucional confiável, por meio da
qual um compromisso possa ser feito para não se construir nenhuma das barragens
planejadas a montante de Belo Monte. Devido à série de precedentes na história
recente de construção de barragens no Brasil, onde o resultado oposto
aconteceu, uma estrutura institucional requereria alguns testes reais antes de
ganhar credibilidade adequada para controlar um caso como Belo Monte, onde as
tentações para voltar atrás em qualquer promessa desse tipo são extraordinariamente
poderosas. Esperar a evolução das instituições ambientais para poder lidar com
a Belo Monte não implica a perda do seu potencial futuro: se nenhuma barragem for
construída no local de Belo Monte nos próximas anos, a opção de se construir
uma barragem lá ainda permanecerá aberta.
Também são necessárias mudanças para
conter o papel das empresas de construção em influenciar as prioridades de
desenvolvimento no favorecimento de grandes obras de infra-estrutura. A grande
atratividade que a Belo Monte tem para a comunidade de barrageiros, poderia
servir, potencialmente, como um bom motivo para induzir todas estas reformulações.
Porém, os perigos são múltiplos, e o risco de dar impulso à construção da
Babaquara paira como uma espada pendurada em cima de todas as discussões de
Belo Monte.
Entre os muitos impactos das
represas a montante que devem ser avaliados, um é o papel delas na emissão de
gases de efeito estufa. Na presente análise, serão apresentadas estimativas
preliminares para as emissões de Belo Monte e de Babaquara. Se as outras quatro
barragens planejadas forem construídas, elas teriam impactos adicionais a serem
considerados.
II.
Hidrelétricas e Emissões de Gases de Efeito Estufa
A Belo Monte está no centro das
controvérsias em curso sobre a magnitude do impacto no aquecimento global das
represas hidrelétricas e sobre a maneira apropriada deste impacto ser
quantificado e considerado no processo de tomada de decisão. Quando os
primeiros cálculos de emissão de gases de efeito estufa das represas existentes
na Amazônia brasileira indicaram impacto significativo (Fearnside, 1995a), esta
conclusão foi atacada, apresentando um caso hipotético que correspondeu à Belo
Monte, com uma densidade energética de mais de 10 Watts de capacidade instalada
por m2 de área de superfície de reservatório (Rosa et al.,
1996). Além de a metodologia adotada provocar cálculos hipotéticos que subestimem
o impacto sobre emissão de gases de efeito estufa, o problema principal é omitir
as emissões da hidrelétrica de Babaquara, com 6.140 km2 rio acima de
Belo Monte (Fearnside, 1996a). Este problema básico permanece hoje, mesmo
depois de muitos avanços em estimativas de emissões de gases de efeito estufa.
A
área relativamente pequena da hidrelétrica de Belo Monte, sozinha, indica que
as emissões de gases de efeito estufa da superfície do reservatório serão
modestas, e quando estas emissões são divididas pelos 11,181 MW de capacidade
instalada da barragem, o impacto parece ser baixo em comparação aos benefícios.
Esta é a razão de se usar a “densidade energética” (Watts de capacidade
instalada por metro quadrado de área d’água) como a medida do impacto de uma
represa sobre o aquecimento global. Apresentando a Belo Monte como uma represa
ideal sob uma perspectiva de aquecimento global, Luis Pinguelli Rosa e
colaboradores (1996) calcularam esta relação como excedendo ligeiramente 10 W/m2,
baseado na área do reservatório originalmente planejada de 1.225 km2
(o índice seria de 25 W/m2 sob as mesmas hipóteses, quando considerada
a área atualmente planejada de 440 km2).
Os regulamentos do Mecanismo de
Desenvolvimento Limpo (MDL) do Protocolo de Kyoto atualmente permitem crédito
de carbono para grandes represas sem restrições, más foi proposto pelo conselho
executivo do MDL, reunindo em Buenos Aires em dezembro de 2004, que estes
créditos sejam restritos a barragens com densidades energéticas de pelo menos
10 W/m2 de área de reservatório (UN-FCCC, 2004, p. 4),
coincidentemente a marca alcançada para Belo Monte segundo o calculo de Rosa et al. (1996). A possibilidade de reivindicar crédito de
carbono para Belo Monte foi levantada em várias ocasiões tanto por funcionários
do governo brasileiro como do Banco Mundial. Uma densidade energética tão alta
quanto 10 W/m2 para Belo Monte requer que esta barragem seja
considerada independente da represa de Babaquara que regularizaria a vazão em
Belo Monte, armazenando água rio acima. A configuração atual para as duas
barragens juntas, com 11.000 + 181,3 + 6.274 = 17.455 MW de capacidade
instalada, e 440 + 6.140 = 6.580 milhões de m2 de área de
reservatório é de 2,65 W/m2 de reservatório. Isto não é muito melhor
que a densidade energética de Tucuruí-I (1,86 W/m2), e muito
inferior ao número mágico de 10 W/m2.
No
caso de Belo Monte, duas razões fazem com que este índice seja altamente
enganador como medida do impacto do projeto sobre o efeito estufa. Primeiro, as
emissões de superfície (que são proporcionais à área do reservatório)
representam apenas uma parte do impacto de aquecimento global de projetos
hidrelétricos: as quantidades de metano liberadas pela passagem da água pelas
turbinas (e vertedouros) dependem muito dos volumes de água que atravessam
estas estruturas. O volume deste fluxo
pode ser grande, até mesmo quando a área do reservatório é pequena, como em
Belo Monte. A segunda razão é que o maior impacto do projeto global é das
represas rio acima. Para cumprir o papel de armazenamento e liberação da água
para abastecer Belo Monte durante a estação seca, as represas a montante devem
ser manejadas com a maior oscilação possível nos seus níveis d’água. Afinal de
contas, se estas barragens fossem usadas “a fio d’água” (i.e., sem oscilações do nível d’água no reservatório) o resultado
não seria nada melhor que o rio sem a vazão regulada, do ponto de vista de
aumentar a produção de Belo Monte. É esta flutuação no nível d’água que faz das
represas rio acima fontes potencialmente grandes de gases de efeito estufa,
especialmente a de Babaquara. É esperada uma variação no nível d’água do
reservatório de Babaquara de 23 m ao longo do curso de cada ano (Brasil,
ELETRONORTE, s/d. [C. 1989]). Para fins de comparação, o nível d’água no
reservatório de Itaipu varia em apenas 30-40 cm. Cada vez que o nível d’água em
Babaquara atingisse seu nível mínimo operacional normal, seria exposto um vasto
lamaçal de 3.580 km2 (aproximadamente o tamanho do reservatório de
Balbina inteiro!). Vegetação herbácea, de fácil decomposição, cresceria
rapidamente nesta zona, conhecida como a zona de “deplecionamento”, ou de
“drawdown”. Quando o nível d’água subisse subseqüentemente, conseqüentemente a
biomassa se decomporia no fundo do reservatório, produzindo metano.
Reservatórios
são estratificados de modo térmico, com uma faixa (termoclino) tipicamente
localizada de 2 a 3 m de profundidade. A temperatura da água diminui
abruptamente abaixo do termoclino, e a água presa debaixo desta camada não se mistura
com a água da superfície. Esta água funda (o hipolimnion) logo se torna
anóxica, e a vegetação herbácea da zona de deplecionamento que se decompõe sob
estas condições produz metano (CH4) em lugar de gás carbônico (CO2).
Uma tonelada de CH4 provoca 21 vezes mais impacto sobre o efeito
estufa que uma tonelada de CO2, se utilizamos o fator de conversão
(potencial de aquecimento global, ou GWP) adotado pelo Protocolo de Kyoto
(Schimel et al., 1996), ou 23 vezes
mais se o valor mais recente calculado pelo Painel Intergovernmental sobre
Mudança do Clima (IPCC) for utilizado (Ramaswamy et al., 2001, pág. 388). Por tonelada (megagrama = Mg) de carbono
liberado em cada forma, CH4 tem 7,6 vezes mais impacto, considerando
o GWP de 21.
Não
se acredita que a madeira nas árvores submersas seja uma fonte significativa de
carbono para a produção de metano porque o tecido vegetal lignificado (madeira)
decompõe-se a uma taxa extraordinariamente lenta sob condições
anaeróbicas. Árvores ainda são
utilizáveis como madeira mesmo depois de permanecerem várias décadas submersas,
como é mostrado pela experiência em Tucuruí onde, 20 anos depois do enchimento
em 1984, a represa ainda é cena de disputas entre vários pretendentes
interessados na exploração do estoque de madeira subaquática. Em contrapartida,
a vegetação herbácea verde decompõe-se rapidamente, liberando assim seu estoque
de carbono na forma de gases, alguns dos quais são liberados para a a
O recrescimento da vegetação na zona de deplecionamento
do reservatório, a cada ano, remove gás carbônico da a
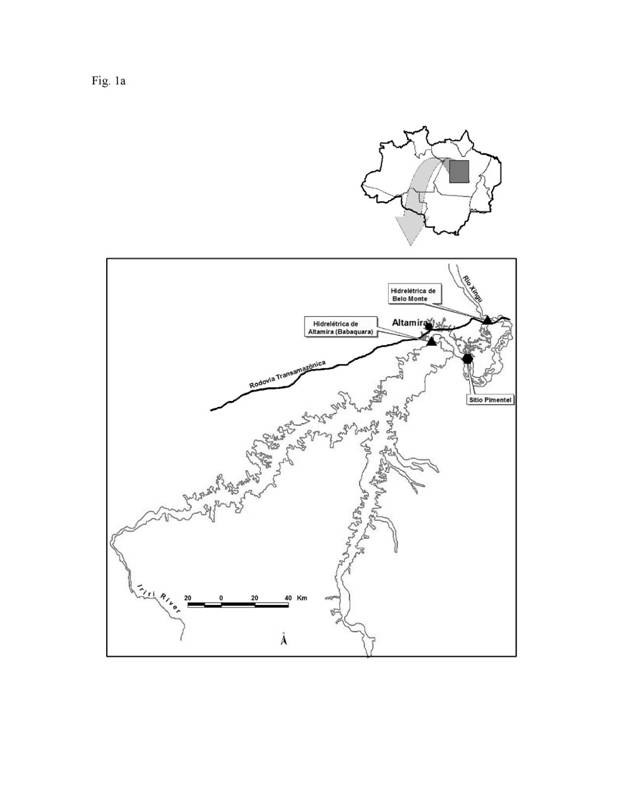
III. Características das Barragens de Belo Monte e
Babaquara
A.) Belo
Monte
A configuração do reservatório de
Belo Monte é altamente incomum, e os cálculos de gases de efeito estufa deveriam
ser desenvolvidos especificamente para estas características. O reservatório é
dividido em duas partes independentes. O “Reservatório da Calha do Rio Xingu”
ocupa o curso do rio Xingu acima da barragem principal, localizada em Sitio
Pimentel (Figura 1). O vertedouro principal tira água deste reservatório, assim
como uma pequena “casa de força complementar” (181,3 MW de capacidade
instalada) que, em períodos de alta vazão, fará uso de parte da água que não
pode ser usada pela casa de força principal. Quantidade maior da água será
desviada a partir da lateral do Reservatório da Calha, por meio de canais de
adução, até o Reservatório dos Canais, ao término do qual se encontram as
tomadas d’água para as turbinas na casa de força principal (11.000 MW). O
Reservatório dos Canais também dispõe de pequeno vertedouro para casos de
emergência. São apresentadas as características dos reservatórios na Tabela 1.
[Figura
1 e Tabela 1 aqui]
Para abastecer as turbinas da
principal casa de força, com capacidade de turbinar 13.900 m3/segundo,
água entrando nos canais fluiria numa velocidade média de 7,5 km/hora num canal
de 13 m de profundidade, levando aproximadamente 2,3 horas para percorrer os 17
km do Reservatório da Calha até o Reservatório dos Canais. Isto será semelhante
a um rio, ao invés de um reservatório. O Reservatório dos Canais, pelo qual a
água levará, em média, 1,6 dias para passar, é de uma forma talvez sem igual na
história de construção de barragens. Em vez do habitual vale inundado, onde a água
flui pelo reservatório que segue a topografia descendente natural de um rio e
seus afluentes, a água no Reservatório dos Canais estará fluindo por uma série
de vales perpendiculares à direção normal de fluxo d’água. A água passará entre
cinco bacias diferentes, na medida em que atravessa os cursos dos igarapés que
terão sido inundados, passando por gargalos rasos quando a água cruza cada um
dos antigos interfluvios. Cada uma destas passagens, algumas das quais serão em
canais escavados como parte do projeto de construção, oferecerá a oportunidade
para quebrar qualquer termoclino que possa ter-se formado nos fundos de vale. É
possível que só água da superfície, relativamente bem oxigenada e de baixo teor
de metano, fará a passagem por estes gargalos, deixando camadas relativamente
permanentes de água rica em metano no fundo de cada vale. Portanto, o
Reservatório dos Canais, de 60 km de comprimento, é uma cadeia de cinco
reservatórios, cada um com um diferente tempo de reposição, sistema associado
de “braços mortos” e potencial para estratificação. Quando a água alcançar o
trecho final antes das tomadas d’água das turbinas, permanecerá lá apenas
durante um tempo curto.
B.)
Babaquara
Em contraste com o volume pequeno do
reservatório e tempo curto de reposição dos dois reservatórios de Belo Monte, o
reservatório de Babaquara tem várias características que o fazem
excepcionalmente nocivo como fonte de metano. Uma é a sua área enorme, do
tamanho de Tucuruí e Balbina juntos. Outra é a área de deplecionamento
extraordinariamente grande que será alternadamente inundada e exposta: 3.580 km2
(Brasil, ELETRONORTE, s/d. [C. 1989]).
O reservatório de Babaquara é
dividido em dois braços, um dos quais terá um tempo de reposição muito lento. O
reservatório inundará os vales dos rios Xingu e Iriri. Medidas grosseiras das
áreas do reservatório (a partir de um mapa no Brasil, ELETRONORTE, s/d. [C.
1988]) indicam que 27% da área de reservatório, aproximadamente, se encontra na
bacia do rio Xingu abaixo da confluência dos dois rios, outros 27% na bacia do
Xingu acima do ponto de confluência e 26% na bacia do rio Iriri. A vazão média
(1976-1995) do rio Iriri é de 2.667 m3/segundo (Brasil, ANEEL,
2001), enquanto a vazão no local da barragem de Babaquara (i.e., abaixo da confluência) é de 8.041 m3/segundo
(Maceira & Damázio, s/d). Presumindo que a porção do reservatório abaixo da
confluência (a porção mais próxima à represa) é três vezes mais funda, então,
em média, com os outros dois segmentos, o tempo de residência no reservatório
de Babaquara da água que desce o rio Xingu é de 164 dias e de 293 dias para a
água que desce do rio Iriri. Embora o tempo de residência seja muito longo em ambos
os casos, tempo bastante para acumular uma grande carga de metano, o tempo para
a parte no Iriri quase alcança o do tempo de residência de 355 dias da notória
represa de Balbina! A tremenda diferença entre Babaquara e Belo Monte, com
oscilações verticais em níveis d’água que variam desde zero no Reservatório dos
Canais de Belo Monte até 23 m em Babaquara, indica que um modelo explícito dos
estoques de carbono e da sua decomposição é necessário, em lugar de uma
extrapolação simples de medidas de concentrações de CH4 e emissões
em outras represas. O modelo desenvolvido para este propósito é descrito nas
seções seguintes.
IV.
Fontes de Carbono e Caminhos de Liberação de Gases de Efeito Estufa
A.) Metano
O
metano produzido por decomposição subaquática pode ser liberado de vários
modos. Uma é a ebulição e a difusão pela superfície do reservatório. Ebulição
permite que o CH4 atravesse a barreira do termoclino, e é altamente
dependente da profundidade da água em cada ponto no reservatório, com emissões
de bolhas muito maiores a profundidades mais rasas. A difusão é importante no
primeiro ano, mas não depois disso; isto porque as populações bacterianas na
água de superfície (epilimnion) aumentam, resultando que qualquer metano que se
difunde por esta camada é oxidado para CO2 antes de alcançar a
superfície (Dumestre et al., 1999;
Galy-Lacaux et al., 1997).
As emissões de superfície também são mais altas nos primeiros anos
depois do enchimento porque o estoque de carbono nas folhas e liteira de foliça
da floresta original e na fração instável do carbono de solo está sendo
liberado do fundo do reservatório na forma de metano. Estes estoques de carbono
iniciais diminuirão na medida em que eles são progressivamente exauridos e, nos
anos posteriores, o carbono somente estará disponível de fontes renováveis,
tais como as macrófitas e o recrescimento na zona de deplecionamento (assim
como também o carbono do solo que entra no reservatório oriundo de erosão rio
acima).
Estão
faltando estudos para quantificar o papel relativo de diferentes fontes de
carbono. No caso do reservatório de Petit Saut, na Guiana francesa, Galy-Lacaux
et al. (1999) acreditam que o carbono
do solo é a fonte principal nos primeiros anos. O estoque de carbono instável
do solo é relativamente grande, comparado aos outros estoques de carbono
facilmente degradado. O presente cálculo usa o estoque de carbono instável
(hidrossolúvel) do solo de 54 Mg C/ha medido nos 60 cm superficiais de um
Ultisolo amazônico típico (Trumbore et al.,
1990, pág. 411). Suposições relativas à taxa de decomposição dos estoques
produzem um total teórico para o carbono liberado na água na forma de CH4.
Considerando o efeito de diluição pelos influxos de água para o reservatório, a
quantidade de carbono que se decompõe anaerobicamente por bilhão de metros
cúbicos de água pode ser calculada. Esta quantidade foi calculada para dois
reservatórios existentes em áreas de floresta tropical (Petit Saut e Tucuruí) e
relacionado à concentração de CH4 na água a uma profundidade
padronizada (30 m) nos mesmos reservatórios.
A quantidade de carbono que se decompõe
anaerobicamente é a soma das porções que se decompõe de folhas originais e
liteira de foliça, carbono instável do solo, macrófitas não encalhadas e
vegetação inundada na zona de deplecionamento. A quantidade de água é o volume
do reservatório ao final do mês, mais os influxos durante o mês e o mês
anterior. A quantidade de carbono que se decompõe anaerobicamente (calculada de
acordo com as suposições dadas acima) relacionada à concentração de CH4
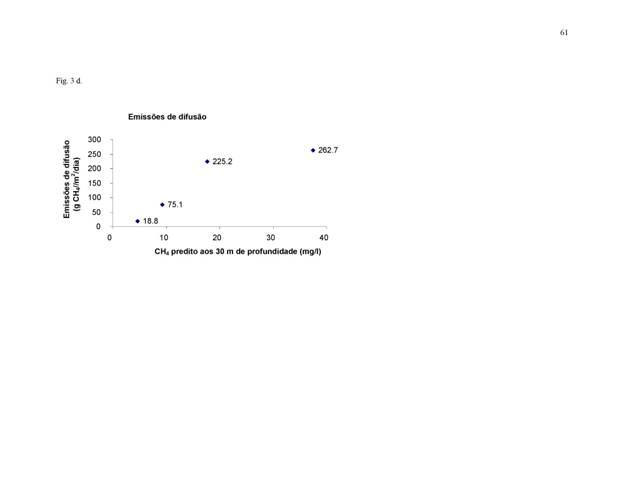
aos 30 m de profundidade é mostrada na Figura 2. Os dados de concentração são de Petit Saut
(Galy-Lacaux et al., 1999), com a
exceção do ponto extremo no lado esquerdo, com 6 mg CH4/litro aos 30
m de profundidade, que é de Tucuruí (J.G. Tundisi, citado por Rosa et al., 1997, pág. 43). A faixa de valores para a quantidade de
carbono que se decompõe anaerobicamente é dividido em três segmentos para o
cálculo da concentração de CH4 aos 30 m de profundidade (equações
1-3).
[Figura 2
aqui]
Para decomposição anaeróbica = 684,4
Mg C/bilhão de m3 de água:
Y = 0,00877 X (eq.
1)
Para decomposição anaeróbica entre
684,5 e 15.000 Mg C/bilhão de m3 de água:
Y = 0,000978 X + 6 (eq. 2)
Para decomposição anaeróbica > 15.000
Mg C/bilhão de m3 de água:
Y = 20 (eq.
3)
Onde: X = decomposição
anaeróbica (Mg C/bilhão de m3 de água)
Y = concentração de CH4
aos 30 m de profundidade (mg/litro)
A
razão entre a concentração de metano a diferentes profundidades e a
concentração aos 30 metros depende da idade do reservatório, já que esta razão
muda com o passar do tempo à medida que as populações bacterianas nas águas de
superfície fiquem mais capazes de degradar o metano para gás carbônico. Dados
do reservatório de Samuel quando isto tinha cinco meses de idade (J.G. Tundisi,
citado por Rosa et al., 1997, pág.
43) são usados para representar reservatórios até 12 meses depois do
enchimento; dados de Petit Saut (Galy-Lacaux et al., 1999) são usados para representar reservatórios do 13º até
o 36º mês, e dados de Tucuruí coletados 44 meses depois do enchimento (J.G.
Tundisi, citado por Rosa et al., 1997,
pág. 43) são usados para representar reservatórios depois do 36º mês. As razões
são calculadas usando as equações na Tabela 2.
[Tabela
2 aqui]
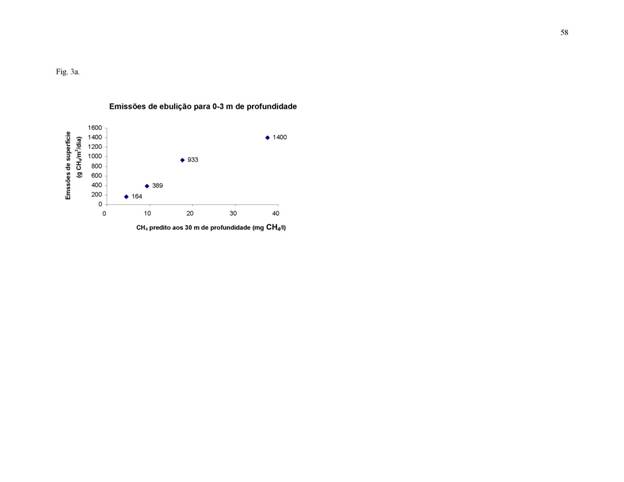
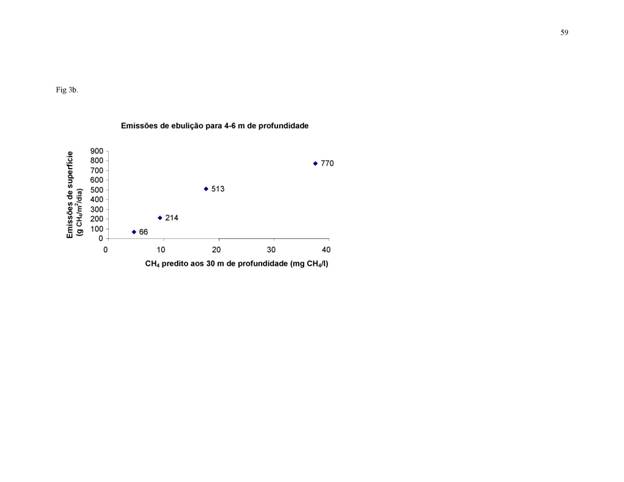
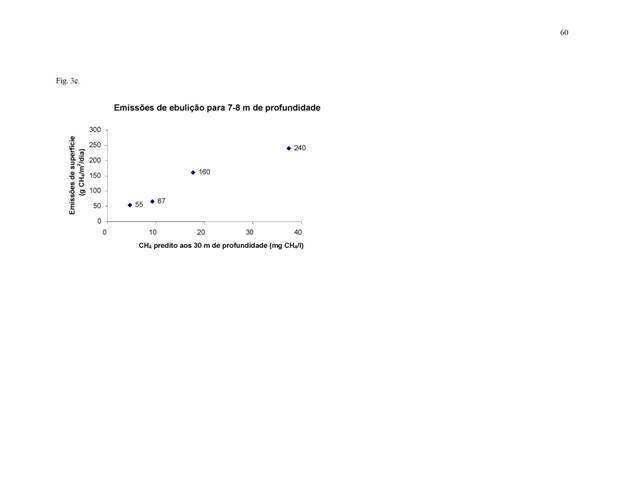
As
emissões de ebulição e de difusão podem ser relacionadas à concentração de CH4
a uma profundidade padronizada de 30 m. A Tabela 3 apresenta equações para
estas emissões para água com profundidades diferentes. Estas razões resultaram
das medidas em Petit Saut (Galy-Lacaux et
al., 1999). A concentração de CH4
prevista aos 30 m de profundidade é estreitamente relacionada às emissões de
ebulição observadas em cada faixa de profundidade nos dados de Petit Saut (0-3
m, 4-6 m e 7-8 m) (Figura 3a, b e c). As emissões de difusão em Petit Saut,
independente da profundidade, também são estreitamente relacionadas à
concentração de CH4 prognosticada aos 30 m (Figura 3d).
[Tabela
3 e Figura 3 aqui]
Usando
os dados derivados acima, as concentrações de CH4 em Babaquara e nos
dois reservatórios de Belo Monte podem ser calculadas. A calibração da
liberação de carbono calculada por decomposição anaerobica aos dados existentes
sobre concentração de CH4 em reservatórios semelhantes é importante
para reduzir qualquer possível viés oriundo das presunções relativas à
magnitude das taxas de decomposição dos vários estoques subaquáticos de
carbono. A água que entra em um reservatório a partir de igarapés e do fluxo normal
do rio, como a água que entra em Babaquara, não contém praticamente nada de CH4,
como foi mostrado pelas medidas em Petit Saut (Galy-Lacaux et al., 1997). No caso de
Belo Monte, no entanto, a água que entra diretamente de Babaquara conterá
quantidades apreciáveis de CH4.
Presume-se
que o manejo d’água em Babaquara siga uma lógica baseada em prover a quantidade
máxima possível de água anualmente a Belo Monte, dentro das limitações
colocadas pelo ciclo sazonal de vazões do rio, o máximo que pode ser usado
pelas turbinas em Babaquara, e o volume de armazenamento vivo do reservatório.
Isto resulta na esperada subida e descida anual do nível d’água. Durante cada
mês ao longo de um período de 50 anos um cálculo é feito da área de zona de deplecionamento
que permanece exposta durante um mês, dois meses, e assim sucessivamente até um
ano, e uma categoria separada que é mantida para área de deplecionamento
exposta durante mais de um ano. A área que é submersa em cada classe de idade é
calculada durante cada mês. Isto permite um cálculo da quantia de biomassa
herbácea que é inundada, baseado em suposições relativas à taxa de crescimento
da vegetação na zona de deplecionamento. A categoria para vegetação com mais de
um ano de idade contém biomassa menos macia, já que o crescimento depois do
primeiro ano é, em grande parte, alocado à produção de madeira, em lugar de
tecidos mais macios (a biomassa de folhas da floresta é usada para esta
categoria).
Macrófitas
são uma fonte importante de biomassa macia, facilmente decomposta. As
populações destas plantas aquáticas aumentam com exuberância para cobrir uma
parte significativa de um reservatório novo, como acontecido em Brokopondo, no
Suriname (Paiva, 1977), Curuá-Una, no Pará (Junk et al., 1981), Tucuruí, no Pará (de Lima, 2002), Balbina, no
Amazonas (Walker et al., 1999), e
Samuel, em Rondônia (Fearnside, s/d-a).
Imagens do satélite LANDSAT indicam que as macrófitas em Tucuruí
cobriram 40% da superfície do reservatório dois anos depois do enchimento,
diminuindo subseqüentemente a 10% depois de uma década (de Lima et al., 2002). Baseado em monitoramento em Samuel e Tucuruí,
Ivan Tavares de Lima (2002) desenvolveu uma equação (eq. 4) para descrever a evolução da cobertura de
macrófitas, que é usada na presente análise:
Y = 0,2 X-0,5 (eq. 4)
onde:
X = anos desde o enchimento
Y = a fração do reservatório coberta por
macrófitas.
As
macrófitas morrem a uma determinada taxa no reservatório e a biomassa morta
afunda. Em lagos de várzea, a mortalidade das macrófitas resulta em uma
reposição da biomassa 2-3 vezes por ano (Melack & Forsberg, 2001, pág.
248). O ponto central desta faixa (4,8 meses) implica que 14,4% da biomassa de
macrófita morrem em cada mês. Esta taxa foi adotada para mortalidade de
macrófita nos reservatórios. Além desta mortalidade, é encalhada uma parte da
biomassa de macrófita quando o nível da água desce. Porque os ventos
prevalecentes (que sopram de leste para oeste) empurrem as macrófitas
flutuantes contra apenas uma margem, uma parte do tapete de plantas flutuantes
necessariamente é posicionada onde será encalhada sempre que o nível d’água
desce. As quantidades envolvidas são impressionantes, como é evidente em
Tucuruí (veja Fearnside, 2001). Porque as macrófitas concentram-se ao longo de
apenas uma margem do reservatório, somente a metade da zona de deplecionamento
é considerada na computação das áreas de macrófitas encalhadas. Quando
encalhadas, as macrófitas morrem e decompõem-se aerobicamente. No entanto, se o
nível d’água sobe novamente antes do processo de decomposição ser completado, o
estoque de carbono remanescente em macrófitas encalhadas é acrescentada ao
estoque de carbono subaquático que pode produzir metano. Aqui se presume que,
se uma área estiver exposta durante apenas um mês, então a metade das
macrófitas encalhadas ainda estará presente quando estas áreas forem reinundadas.
A cobertura de macrófitas em
reservatórios amazônicos sofre uma sucessão regular de espécies, começando com Eicchornia e terminando com Salvinia, como aconteceu em Curuá-Una
(Vieira, 1982) e Balbina (Walker et al.,
1999). Eicchornia e outras espécies que predominam nos primeiros anos têm significativamente mais biomassa por
hectare que Salvinia. Em Balbina a
substituição de macrófitas de biomassa alta por Salvina aconteceu entre o sétimo e o oitavo ano depois do
enchimento (Walker et al., 1999, pág.
252). Nos presentes cálculos presume-se
que a troca para Salvinia acontece
sete anos depois de enchimento do reservatório para as represas do Xingu.
Macrófitas flutuantes como Eicchornia
e Salvinia são muito comuns em
reservatórios, mas algumas espécies enraizadas também ocorrem.
Presume-se que a biomassa de
macrófitas é de 11,1 Mg/ha de peso seco durante os primeiros seis anos, baseado
em um tapete de Eicchornia mensurado
em Lago Mirití, um lago de várzea perto de Manacapuru, Amazonas (P.M.
Fearnside, dados não publicados). Para comparação, em lagos de várzea, espécies
de Oryza tiveram 9-10 Mg/ha de peso
seco, enquanto Pasalum teve 10-20
Mg/ha (T.R. Fisher, D. Engle & R. Doyle, dados inéditos citados por
Melack & Forsberg, 2001, pág. 248). Em outra medida em lagos de várzea
(onde a disponibilidade nutrientes é maior como nas represas no Xingu), nove
medidas de macrófitas enraizadas na várzea depois de aproximadamente três meses
de crescimento resultaram em uma média de 5,7 Mg/ha de biomassa seca (DP=1,7,
variação=3,2-8,7) (Junk & Piedade, 1997, pág. 170). O valor presumido de 11,1 Mg/ha nas represas
do Xingu está na faixa para biomassa de macrófitas flutuantes e submersas em
outras partes do mundo. Por exemplo, as macrófitas submersas em Lago Biwa, no
Japão tem 7-10 Mg/ha de biomassa seca (Ikusima, 1980, pág. 856).
Depois que a transição
para Salvina acontece, a biomassa por
hectare de macrófitas é mais baixa. O valor de biomassa usado no cálculo é de 1,5 Mg/ha de peso seco que é
a biomassa de tapetes de Salvinia
auriculata (Junk & Piedade, 1997, pág. 169).
O
metano da água que é presa debaixo do termoclino será exportado dos
reservatórios na água puxada pelas turbinas e pelo vertedouro. Esta é uma
característica de represas hidrelétricas, completamente diferente dos corpos
d’água naturais, tais como lagos de várzea, que são fontes globalmente
significativas de CH4 apenas com emissões de superfície. Abrir as
entradas para as turbinas e para o vertedouro é como tirar a tampa do ralo em
uma banheira: a água é tirada do fundo, ou pelo menos da porção mais funda
(hipolimnion) do reservatório. Debaixo do termoclino a concentração de CH4
aumenta à medida que se desce na coluna d’água. Uma observação importante de
Petit Saut é que, dentro de um mesmo reservatório, a concentração de CH4,
em qualquer determinado ponto é aproximadamente constante a qualquer dada
profundidade abaixo da superfície, independente da profundidade até o fundo do
local em questão (Galy-Lacaux et al.,
1997). A presente análise calcula para
cada mês a profundidade abaixo da superfície do vertedouro e das entradas da
turbina, para então calcular a concentração de CH4 correspondente na
água liberada por estas estruturas.
À
medida que se desce pela coluna d’água, a pressão aumenta e a temperatura
diminui. Ambos efeitos agem para aumentar a concentração de CH4 a
profundidades maiores. Pela Lei de Henry, a solubilidade de um gás é
diretamente proporcional à pressão, enquanto o Princípio de Le Chatelier reza
que a solubilidade de um gás é inversamente proporcional à temperatura. Embora
ambos os efeitos sejam importantes, o efeito da pressão predomina (Fearnside,
2004). A pressão é quase cinco a
A
fração do CH4 dissolvido que é liberado no transcurso da água pelo
vertedouro e pelas turbinas dependerá da configuração destas estruturas. No
caso do vertedouro em Babaquara, a queda de 48 m depois de emergir das
comportas (Tabela 1) deveria garantir uma liberação praticamente completa. No
caso das turbinas, porém, alguma parte do conteúdo de CH4
provavelmente será repassada para o reservatório de Belo Monte, imediatamente a
jusante de Babaquara. O reservatório de Belo Monte é planejado para chegar até
o pé da barragem de Babaquara, fazendo com que seja injetada a água que emerge
das turbinas de Babaquara diretamente no reservatório de Belo Monte, em lugar
de fluir em um trecho de rio normal antes de entrar no reservatório. Como a
água puxada do fundo da coluna d’água do reservatório de Babaquara estará a
baixa temperatura, provavelmente afundará imediatamente no hipolimnion uma vez
que entra diretamente no reservatório de Belo Monte. Seu conteúdo de CH4
seria, então, parcialmente preservado, e estaria sujeito a liberação quando a
água emergir posteriormente das turbinas de Belo Monte.
B.) Gás carbônico
Diferente
do metano, o gás carbônico é tirado da a
A biomassa de madeira acima d’água é modelada em algum detalhe, baseado
no que é conhecido a partir da experiência em Balbina (que foi enchido ao longo
do período 1987-1989). Os troncos das árvores se partem no ponto atingido pelo
nível alto da água, deixando tocos projetando fora da água quando o nível decai.
Até oito anos depois de ser inundadas, aproximadamente 50% das árvores de ≥
25 cm de diâmetro e 90% das árvores de < 25 cm de diâmetro tinham-se partidos
(Walker et al., 1999). Além disso, os galhos continuamente caem das
árvores em pé. Aproximadamente 40% das árvores de terra firme flutuam em água
(veja Fearnside, 1997a). As árvores que se afundam permanecem onde elas estão,
seja na zona permanentemente inundada ou nas áreas mais rasas que estão
periodicamente expostas na zona de deplecionamento. Os troncos que flutuam são
empurrados pelo vento e pelas ondas até a margem e serão expostas à
decomposição aeróbia na zona de deplecionamento quando o nível d’água descer.
São calculados os estoques e as taxas de decomposição para cada categoria. A
decomposição aeróbica contribui para a emissão de CO2 da biomassa
acima da água. Parâmetros para a dinâmica e decomposição aeróbica da biomassa
acima d’água são apresentados na Tabela 4.
[Tabela
4 aqui]
As emissões de biomassa acima d’água consideradas aqui são
conservadoras por duas razões. Uma é que elas estão baseadas na vazão média do
rio em cada mês e na suposição de que o manejo da água respeite o limite do
nível mínimo normal previsto para o reservatório. Nenhuma consideração foi feita
quanto à possibilidade de que o nível da água poderia ser abaixado além deste
nível mínimo em anos extremamente secos, como em eventos de El Niño. A outra
suposição conservadora é que a biomassa na zona de deplecionamento nunca se queima.
Queimar é um evento ocasional, mas afeta quantidades significativas de biomassa
quando isso acontecer. Durante a seca do El Niño de 1997-1998, os reservatórios
de Balbina e de Samuel atingiram cotas muito inferiores aos níveis de operação
oficialmente tidos como “mínimos”, e áreas grandes das zonas de deplecionamento
expandidas se queimaram. Embora seja provável que tais emissões às vezes
acontecerão em Babaquara, elas não foram considerados nesta análise.
Outra
fonte de emissões é de árvores perto da margem do reservatório, mortas quando o
lençol d’água sobe e alcança as suas raízes. Em Balbina, uma faixa de árvores
mortas é evidente ao redor da margem do reservatório (Walker et al., 1999). Porque o formato do contorno da margem é
extremamente tortuoso e inclui as margens das muitas ilhas criadas pelo
reservatório, esta faixa de mortalidade da floresta afeta uma área
significativa. As árvores mortas se decompõem, liberando CO2, e, ao
longo de um período de décadas, uma floresta secundária se desenvolve (com uma
absorção de carbono). A presente análise presume que a mortalidade é de 90% na
faixa até 50 m além da margem do reservatório e de 70% na faixa entre 50 a 100
m dessa margem. A decomposição segue o mesmo curso que em áreas derrubadas para
agricultura, e presume-se que a floresta secundária cresça à mesma taxa que as
capoeiras em pousios de agricultura itinerante (Fearnside, 2000).
V.
Emissões de Ecossistema de Pre-represa
As
emissões dos ecossistemas presentes antes das represas serem construídas devem
ser deduzidas das emissões das represas para se ter uma avaliação justa do
impacto líquido do desenvolvimento hidrelétrico. A idéia de que as florestas
inundadas pelos reservatórios têm emissões naturais grandes de gases de efeito
estufa foi um dos principais componentes do ataque que a indústria hidrelétrica
montou contra estudos que indicam emissões altas das represas hidrelétricas.
Quando os primeiros estudos indicaram que a hidrelétrica de Balbina emitiu mais
do que seria liberado produzindo a mesma quantidade de eletricidade a partir de
combustíveis fósseis (Fearnside, 1995a), a Associação Nacional de Hidrelétricas
dos EUA (USNHA) reagiu com a declaração:
“É uma asneira e
é muito exagero ... O metano é produzido bastante substancialmente na floresta
tropical e ninguém sugere cortar a floresta tropical.”
Esta declaração de Karolyn
Wolf (porta-voz da USNHA) ilustra bem a veemência com que se resistiu a este
assunto (veja
As áreas dos ecossistemas naturalmente inundados e não
inundados são apresentadas na Tabela 5. Os tipos de floresta sazonalmente
inundados são considerados como pertencendo à “área inundada”. No entanto, isto pode representar uma superestimativa
da extensão verdadeira “área inundada”, sendo que imagens de radar do Satélite
de Recursos da Terra Japonês (JERS) indicam que praticamente nada da área do
reservatório planejado tem inundação abaixo da cobertura da floresta (veja
Melack & Hess, 2004). No entanto, deveria ser lembrado que lagos
temporários ao longo dos rios Xingu e Iriri existem: mapas analisados por de
Miranda et al. (1988, pág. 88)
indicam de 28 a 52 lagos na área a ser inundada por Babaquara, dependendo do
mapa usado na análise.
[Tabela
5 aqui]
Os parâmetros
para emissões de metano pela floresta não inundada (floresta de terra firme) são
apresentados na Tabela 6. Estes indicam um efeito mínimo sobre o metano, com a
perda de um sumidouro pequeno no solo quando inundado. Emissões de óxido nitroso (N2O) em
solo florestado não inundado são pequenas: 0,0087 Mg de gás/ha/ano (Verchot et al., 1999, pág. 37), ou 0,74
Mg/ha/ano de carbono CO2-equivalente, considerando o potencial de
aquecimento global de 310 (Schimel et al.,
1996, pág. 121). Cálculos de óxido
nitroso para floresta não inundada e para áreas inundadas são apresentados na
Tabela 7. Os cálculos incluem o efeito da formação de poças temporárias em
áreas de terra firme durante eventos periódicos de chuva pesada (Tabela 7).
[Tabelas
6 e 7 aqui]
Para
áreas inundadas, é feita a suposição de que cada ponto inundado é submerso
durante dois meses, em média, por ano. Claro que algumas partes da área ficariam
submersas mais tempo e algumas durante períodos mais curtos, dependendo da
altitude de cada ponto. O valor usado para emissões por hectare (103,8 mg CH4/m2/dia,
DP=74,1, variação=7-230) é a média de cinco estudos em floresta de várzea de
água branca revisada por Wassmann e Martius (1997). Um valor semelhante de 112
mg CH4/m2/dia (n=68, DP=261) foi encontrado durante
inundações em florestas de água preta (igapós) ao longo do rio Jaú, um afluente
do rio Negro. Nas florestas de igapó na bacia do rio Jaú estudadas por
Rosenqvest et al. (2002, pág. 1323) a
taxa de emissão de metano das áreas inundadas é muito mais alta durante o
período curto quando o nível d’água estiver caindo do que durante o resto do
tempo que a área está debaixo d’água. Isto tenderia a fazer a emissão anual um
pouco independente do período de tempo que as áreas são inundadas, e torna o
resultado relativamente robusto quando extrapolado para outras bacias
hidrográficas na Amazônia se expressado em termos de emissão por ciclo de
inundação (em lugar de por dia inundado). Presumindo as mesmas taxas de emissão
como as medidas nos estudos de várzea de água branca (o Xingu é considerado um
rio de água clara, mais semelhante à água branca do que água preta), a emissão
anual seria equivalente a apenas 0,043 milhões de toneladas de carbono
equivalente a carbono de CO2 em Babaquara em uma base diária, ou
0,248 milhões de toneladas de carbono CO2-equivalente se este
resultado for multiplicado por três para aproximar o efeito da estação de
enchente mais curta (2 meses contra 6 meses). Os ajustes resultantes para o
efeito dos ecossistemas pré-represa são muito pequenos, como será mostrado mais
adiante quando serão calculadas as emissões líquidas para as duas represas.
VI.
Emissões de Construção
Represas, obviamente, requerem muito mais materiais,
como aço e cimento, do que instalações equivalentes movidas a combustível
fóssil, como as usinas termoelétricas a gás que estão sendo construídas
atualmente em São Paulo e em outras cidades no Centro-Sul brasileiro. São calculadas as quantidades de aço
usadas na construção de Belo Monte na Tabela 8.
Para Babaquara, supõe-se que a quantidade de aço usada em equipamento
eletromecânico é proporcional à capacidade instalada, enquanto presume-se que a
quantidade de aço em concreto armado é proporcional ao volume de concreto. As
quantidades são calculadas em proporção às quantidades usadas em Belo Monte
(Tabela 8).
[Tabela
8 aqui]
A
quantidade de cimento usada em cada barragem é determinada na Tabela 9. A Belo
Monte é excepcionalmente modesta no uso de cimento porque o local permite que a
barragem principal (Sitio Pimentel) seja construída em um local que é mais alto
em elevação que a casa de força principal (o Sitio Belo Monte). A barragem
principal tem uma altura máxima de apenas 35 m (Brasil, ELETRONORTE, 2002, Tomo
I, pág. 6-33), enquanto a casa de força principal aproveita uma queda de
referência de 87,5 m (Brasil, ELETRONORTE, 2002, Tomo I, pág. 3-52). A maioria dos projetos hidrelétricos, como
Babaquara ou Tucuruí, tem a casa de força localizada ao pé da própria barragem,
e portanto só gera energia de uma queda que corresponde à altura da barragem
menos uma margem pequena para borda livre ao topo. Tucuruí, que é até agora a
“campeã” de todas obras públicas brasileiras em termos de uso de cimento, usou
três vezes mais cimento do que a quantidade prevista para Belo Monte (Pinto,
2002, pág. 39). A Babaquara usaria 2,6
vezes mais cimento por MW de capacidade instalada do que a Belo Monte (Tabela
9).
[Tabela
9 aqui]
É esperado que a quantidade de
diesel usada para Belo Monte seja 400 ×103 Mg (Brasil, ELETRONORTE,
2002, Tomo II, pág. 8-145).
Isto inclui um ajuste das unidades (como informado no estudo de viabilidade)
para trazer os valores dentro da faixa geral de uso de combustível em outras
barragens (por exemplo, Dones & Gantner, 1996 calcularam um uso médio de 12 kg diesel/TJ
para barragens na Suíça). O estudo de viabilidade contém várias inconsistências internas nas unidades, que
presumivelmente resultaram de erros tipográficos. A Belo Monte exige uma quantidade
bastante grande de escavação por causa da necessidade para cavar o canal de
adução que conecta o Reservatório da Calha ao Reservatório dos Canais, e várias
escavações menores são projetadas nos gargalos dentro do Reservatório dos
Canais. A quantidade esperada de escavação para estes canais aumentou
substancialmente entre a versão do estudo da viabilidade de 1989 e a de 2002
porque foram descobertos erros na cartografia topográfica da área (Brasil,
ELETRONORTE, 2002, Tomo I, pág. 8-22).
Para Babaquara presume-se que o uso de diesel será proporcional à
quantidade de escavação planejada naquela represa, (da Cruz, 1996, pág.
18).
As estimativas de materiais para
construção de represas e linhas de transmissão são apresentadas na Tabela 10.
Os totais resultantes (0,98 milhões de Mg C para a Belo Monte e 0,78 milhões de
Mg C para Babaquara) são muito pequenos comparado às emissões posteriores dos
reservatórios. Não foram deduzidas destes totais as emissões da construção das
termoelétricas a gás equivalentes. A emissão de construção de instalações de
gás natural é mínima: uma análise de ciclo de vida de usinas a gás de ciclo
combinada em Manitoba, Canadá indica emissões de CO2 de construção
de apenas 0,18 Mg equivalente/GWh (McCulloch & Vadgama, 2003, pág. 11).
[Tabela
10 aqui]
VII.
Emissões Calculadas da Belo Monte e Babaquara
O
cálculo das emissões de gases de efeito estufa requer um cenário realista para o
cronograma do enchimento e da instalação das turbinas em Belo Monte e
Babaquara, e para as políticas de manejo de água nas duas represas. Aqui se
presume que Babaquara será enchida sete anos após Belo Monte (i.e., que Belo Monte opera usando a
vazão não regularizada do rio antes deste tempo). Este cronograma corresponde
ao cenário menos-otimista no plano original (veja Sevá, 1990). As turbinas em
ambas as represas serão instaladas a uma taxa de uma a cada três meses, ri
O
presente cálculo segue os planos para enchimento do reservatório indicados no
estudo de viabilidade. O Reservatório dos Canais será enchido primeiro até um
nível de 91 m sobre o nível médio do mar. Isto será feito depois que a primeira
enchente passar pelo vertedouro (Brasil, ELETRONORTE, 2002, pág. 8-171). Presume-se
que isto aconteça no mês de julho. A casa de força complementar será usada,
então, a este nível reduzido do reservatório durante um ano antes da casa de
força principal estar pronta para uso, como planejado no Plano Decenal de
ELETROBRÁS (Brasil, MME-CCPESE, 2002). O cenário de referência do Plano Decenal
estima o começo de operação da casa de força complementar para fevereiro de
2011 e da casa de força principal para março de 2012.
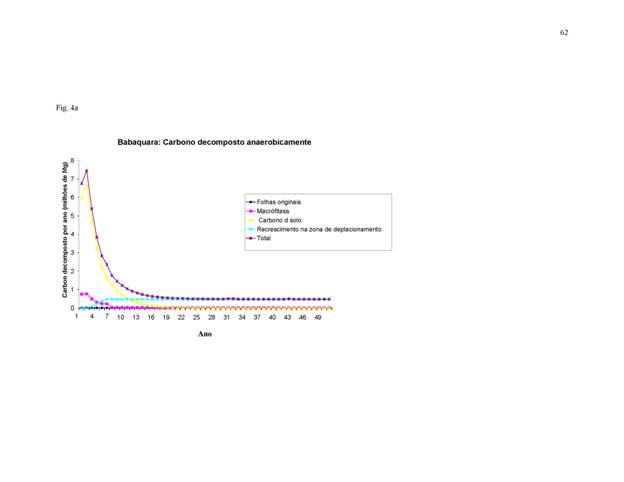
Os
resultados de um cálculo de 50 anos das fontes de carbono em formas facilmente
degradadas para cada reservatório são apresentados na Figura 4. É evidente que
todas as fontes são muito mais altas nos primeiros anos do que nos anos
posteriores. Os estoques de carbono instável do solo, biomassa de madeira acima
d’água e árvores mortas ao longo da margem diminuem, reduzindo assim as
emissões destas fontes. As macrófitas diminuem, mas não desaparecem, provendo assim
uma fonte em longo prazo que, nos anos posteriores, é de maior importância
relativa, embora de menor em termos absolutos. O recrescimento da vegetação na
zona de deplecionamento representa uma fonte estável em longo prazo de carbono
de fácil degradação que aumenta em importância relativa a medida que as outras
fontes declinem.
[Figura
4 aqui]
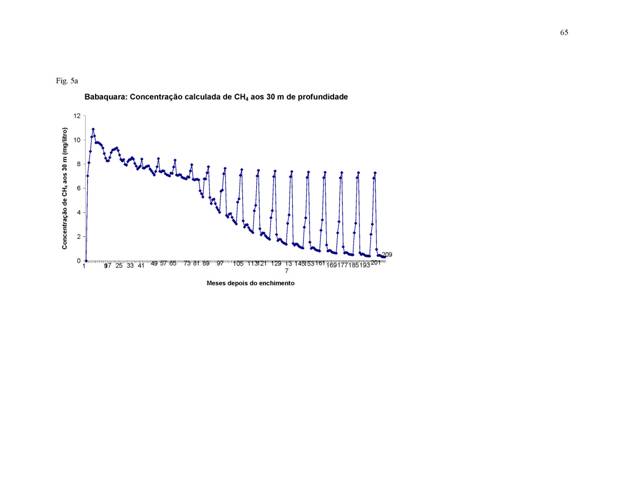
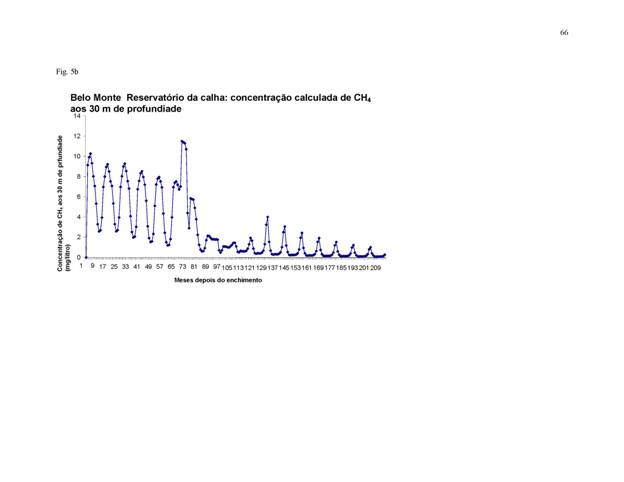
São
mostradas as concentrações de metano calculadas a uma profundidade padronizada
de 30 m para cada reservatório na Figura 5. Estas concentrações calculadas
seguem a tendência geral de oscilação sazonal e declínio assintótico observada
em valores medidos em Petit Saut (Galy-Lacaux et al., 1999, pág. 508). As
oscilações são muito grandes em Babaquara depois que as diferentes fontes de
carbono da vegetação de deplecionamento diminuíssem em importância (Figura 5a).
São mantidos os picos grandes em concentração de metano em Babaquara, seguido
por uma diminuição das concentrações durante o resto de cada ano. Os picos
altos são mantidos porque o carbono vem da inundação de vegetação de deplecionamento
quando a água sobe. Os picos de concentração resultam em emissões
significativas porque estes períodos correspondem a períodos de fluxo alto de
turbina para maximizar produção de energia.
[Figura
5 aqui]
As
emissões por diferentes caminhos para o complexo Belo Monte/Babaquara como um
todo são mostradas na Figura 6. Biomassa acima d’água e mortalidade de árvores
na margem diminuem até níveis insignificantes ao longo do período de 50 anos,
mas a grande magnitude das emissões de biomassa acima d’água nos primeiros anos
dá para esta fonte um lugar significativo na média de 50 anos. Cinqüenta anos
geralmente são o período de tempo adotado pela indústria hidrelétrica em
discussões da “vida útil” de represas, e cálculos são feitos freqüentemente,
financeiro e ambiental, neste horizonte de tempo, como nos regulamentos aplicáveis
em estudos de viabilidade para represas no Brasil (Brasil, ELETROBRÁS &
DNAEE, 1997). As represas amazônicas existentes, particularmente Tucuruí,
Balbina e Samuel, eram relativamente jovens em 1990, o ano padrão mundial de
referência para os inventários dos gases de efeito estufa, designados pela
Convenção Quadro das Nações Unidas sobre Mudanças do Clima e o ano usado para
vários cálculos anteriores de emissões de gases de efeito estufa (Fearnside,
1995a, 1997b, 2002a, s/d-a,b). As emissões em 1990 eram então bastante altas, e
a indústria hidrelétrica freqüentemente tem contestado que estas estimativas
dão um quadro negativo demais ao papel de hidrelétricas no efeito estufa (por
exemplo, IHA, s/d [C. 2002]). Os cálculos
atuais mostram que, mesmo ao longo de um horizonte de tempo de 50 anos, o
impacto sobre o aquecimento global de uma represa como Babaquara é significativo.
[Figura
6 aqui]
VIII. Incertezas Fundamentais
Um cálculo como o do presente estudo para o
complexo Belo Monte/Babaquara envolve muita incerteza. Não obstante, o cálculo
precisa ser feito, e as melhores informações disponíveis devem ser usadas para
cada um dos parâmetros requeridos pelo modelo. Na medida em que pesquisas nesta
área procedem, estimativas melhores para estes parâmetros se tornarão
disponíveis, e o modelo poderá interpretar rapidamente estas informações em
termos do resultado delas sobre as emissões de gases de efeito estufa.
Embora um conjunto completo de
testes de sensitividade não tenha sido administrado ainda, o comportamento do
modelo fornece várias indicações sobre quais parâmetros são os mais
importantes. Nos primeiros anos depois de encher o reservatório, emissões são
dominadas pelo CO2 liberado pela decomposição da biomassa situada
acima da água. Estas emissões, embora sujeitas à incerteza, são fundadas nos
melhores dados disponíveis sobre decomposição em áreas desmatadas. Embora sejam
valiosas medidas específicas de árvores em reservatórios, uma mudança radical
no resultado não é esperada. As presunções sobre mortalidade da floresta a
diferentes distâncias da margem são apenas suposições, mas neste caso a
quantidade de carbono envolvido é insuficiente para fazer qualquer diferença
significativa no resultado global.
Os anos iniciais também incluem uma
emissão significativa da liberação de metano pelo transcurso da água pelas
turbinas. Para a porcentagem do metano dissolvido que é liberado no cenário de
baixas emissões adota-se os valores derivados de medidas em Petit Saut
(Galy-Lacaux et al., 1997,
1999). Por causa de diferenças entre
Petit Saut e as represas brasileiras, a faixa usada é muito larga (21-89,9%)
(Veja a discussão em Fearnside, 2002a). As estimativas de emissões aqui apresentadas
são os pontos médios entre os extremos dos resultados produzidos para a
porcentagem emitida junto às turbinas. Acredita-se que este valor médio seja
conservador.
Deve ser lembrado que, quando Belo
Monte e Babaquara entrarem em operação, haverá uma certa compensação entre as duas
represas que reduz o efeito global da incerteza relativo à porcentagem de
metano dissolvido que é liberado junto às turbinas. Quando for usada uma baixa
estimativa para este parâmetro, a emissão em Babaquara fica reduzida, mas o CH4
não liberado é repassado para a Belo Monte, onde por conseguinte aumentam
as emissões por outros caminhos (emissões de superfície e emissões no canal de
adução e nos gargalos).
As fontes de carbono para emissões
de CH4 nos primeiros anos são dominadas por liberação de carbono instável
do solo (Figura 4). Embora faltem medidas desta liberação para qualquer
reservatório, a evolução dos valores para emissão aos valores para concentração
de CH4 aos 30 m de profundidade, usando valores observados nesta
faixa nos primeiros anos, especialmente em Petit Saut, resulta em uma
trajetória realística de concentrações de CH4 e de emissões desta
fonte.
Mais importantes são as incertezas
relativas à emissão de CH4 depois que o pico inicial passe. Muito
menos dados de reservatórios amazônicos mais velhos estão disponíveis para
calibrar esta parte da análise. O declínio em áreas de macrófita reduz a
importância da incerteza relativa a esta fonte para as emissões em longo prazo.
O que predomina para o complexo como um todo é a biomassa da zona de deplecionamento
em Babaquara. Isto resulta em picos sazonais grandes na concentração de CH4
no reservatório de Babaquara (Figura 5a). Uma parte deste metano é repassada
para os dois reservatórios de Belo Monte (Figura 5b e 5c). A taxa de crescimento
da vegetação na zona de deplecionamento é, então, crítica, e nenhuma medida
atual disto existe. A suposição feita é de que este crescimento acontece
linearmente, acumulando 10 Mg de matéria seca em um ano. O valor usado para o conteúdo de carbono
desta e das outras formas de biomassa macia é de 45%. A taxa de crescimento presumida
é extremamente conservadora, quando comparada às taxas de crescimento anuais
medidas de plantas herbáceas para o período de três meses de exposição em áreas
de várzea ao longo do rio Amazonas perto de Manaus: em 9 medidas por Junk &
Piedade (1997, pág. 170) estas plantas acumularam, em média, 5,67 Mg/ha de peso
seco (DP=1,74, variação=3,4-8,7). O valor proporcional para um ano de
crescimento linear seria 22,7 Mg/ha, ou mais que o dobro do valor presumido
para a zona de deplecionamento de Babaquara. Uma medida da biomassa acima do
solo de gramíneas até 1,6 meses após a exposição de terras de várzea no Lago
Mirití indica uma taxa de acúmulo de matéria seca equivalente a 15,2 Mg/ha/ano
(P.M. Fearnside, dados não publicados). A fertilidade do solo nas zonas de
sedimentação de várzea é maior do que em zona de deplecionamento de um
reservatório, mas uma suposição da ordem de metade da taxa de crescimento da
várzea parece segura. Não obstante, este é um ponto importante de incerteza no
cálculo.
Taxas de decomposição também são
importantes, e medidas sob condições anaeróbicas em reservatórios não são
disponíveis. Acredita-se que a
decomposição da vegetação herbácea na várzea oferece um paralelo adequado. Em
medidas sob condições inundadas em várzea de água branca, a decomposição de
três espécies (Furch & Junk, 1997, pág. 192; Junk & Furch, 1991) e uma
experiência em um tanque de 700 litros com uma quarta espécie (Furch & Junk,
1992, 1997, pág. 195) indicaram a fração de peso seco perdida depois de um mês
de submersão, em média, de 0,66 (DP = 0,19 variação=0,425-0,9). O valor mais
baixo (0,425) é da espécie medida na experiência no tanque, onde a anoxiada água
foi constatada depois de aproximadamente um dia. Se as medidas sob condições naturais
incluíssem alguma decomposição aeróbia, a taxa média para condições totalmente
anóxicas poderia ser um pouco abaixo da média para as quatro espécies usadas
aqui.
As taxas de decomposição aeróbica
para macrófitas encalhadas determinam o quanto dessa biomassa ainda esteja
presente se o nível d’água fosse subir novamente antes da decomposição ser
completa. Uma medida de morta em Lago
Mirití até 1,6 mês após o encalhamento indica uma perda de 31,4% do peso seco
por mês (P.M. Fearnside, dados não publicados). O número de observações é mínimo (três
parcelas de 1 m2).
O manejo da água em Babaquara também
é importante para determinar a quantidade de emissão da zona de deplecionamento.
Quanto mais tempo o reservatório seja mantido a um nível baixo, mais vegetação
cresce na zona de deplecionamento. A liberação subseqüente de CH4
quando a zona de deplecionamento for inundada mais que compensa para o efeito
na direção oposta que os baixos níveis d’água têm na redução da profundidade até a entrada da
turbina em Babaquara, e, portanto, na concentração de CH4 na água
que passa pelas turbinas. As presunções para uso d’água utilizadas no cálculo
resultam em três meses de níveis baixos de água, quatro meses de níveis altos e
cinco meses de níveis intermediários.
A magnitude dos picos sazonais altos
de CH4 depende da relação entre a quantidade de carbono que degrada
e o estoque (e concentração) de CH4 quando estas variáveis estavam
em níveis altos nos primeiros anos em Petit Saut (i.e., dados de Galy-Lacaux et
al., 1997, 1999). A natureza da
fonte de carbono em Petit Saut durante este tempo era diferente (acredita-se
ter sido principalmente carbono do solo). A verdadeira quantidade de carbono
degradada anaerobicamente em Petit Saut durante este tempo é desconhecida, e o
escalamento que empresta confiança aos resultados durante os anos iniciais
depois de reservatório encher, quando as fontes de carbono eram do mesmo tipo,
não dá tanta confiança a estes resultados para os anos posteriores. Quantificar
a relação entre a produção de CH4 e a quantidade de decomposição de
biomassa macia (como as macrófitas e especialmente a vegetação da zona de deplecionamento)
deveria ser uma prioridade para pesquisa. No entanto, o resultado geral, isto
é, que a vegetação da zona de deplecionamento produz um pulso grande e
renovável de CH4 dissolvido em reservatórios, não há dúvida. Um caso
relevante é a experiência na hidrelétrica de Três Marias, no Estado de Minas
Gerais, onde uma flutuação vertical de 9 m no nível da água resultou na
exposição e inundação periódica de uma zona de deplecionamento grande, com um
pico grande subseqüente de emissões de metano pela superfície do lago (Bodhan
Matvienko, comunicação pessoal, 2000). Até mesmo na idade muito avançada de 36
anos, o reservatório de Três Marias emite metano por ebulição em quantidades
que excedem em muito as emissões de superfície de todos os outros reservatórios
brasileiros que foram estudados, inclusive Tucuruí, Samuel e Balbina (Rosa et al., 2002, pág. 72).
Uma fonte adicional de incerteza é o
destino da carga dissolvida de CH4 quando a água atravessa os 17 km
do canal de adução de Belo Monte e pelos quatro conjuntos de gargalos que
separam as pequenas bacias hidrográficas inundadas que compõem o Reservatório
dos Canais. Parte do metano é emitida, parte é oxidada, e o resto é passado
para o Reservatório dos Canais. Os parâmetros usados para isto estão baseados
na suposição de que o canal (largura na superfície de aproximadamente 526 m,
com um fluxo em plena capacidade de 13.900 m3/segundo) é semelhante
ao trecho do rio Sinnamary, na Guiana francesa, abaixo da barragem de Petit
Saut (onde a largura média do rio é 200 m e a vazão média é apenas 267 m3/segundo).
Galy-Lacaux et al. (1997) calcularam
concentrações de metano e fluxos ao longo de 40 km de rio abaixo da barragem de
Petit Saut e calcularam as quantidades emitidas e oxidadas no rio. Os
resultados deles indicam que, para o CH4 dissolvido que entra do rio
oriundo da represa, são liberados 18,7% e são oxidados 81,3% (média de medidas
em três datas, com a porcentagem liberada variando de 14 a 24%). Praticamente
toda a liberação e oxidação acontecem dentro nos primeiros 30 quilômetros. No
rio Sinnamary, depois de uma extensão inicial de 4 km onde um processo de mistura
acontece, a concentração de CH4 na água e o fluxo da superfície diminuem
linearmente, chegando a zero a 30 km abaixo da barragem (i.e., ao longo de uma extensão de rio de 26 km). Considerando o
estoque a cada ponto ao longo do rio, pode-se calcular que, nos primeiros 17 km
de rio, são liberados 15,3% do CH4 e são oxidados 66,5%. No cálculo
para Belo Monte presume-se que estas porcentagens se aplicam ao canal de
adução, e que o metano restante é repassado para o Reservatório dos Canais.
Estimativas para emissão nos
gargalos foram derivadas a partir de informações sobre o comprimento deles e as
porcentagens de emissão e oxidação que aconteceram ao longo de uma extensão de
rio de mesmo comprimento abaixo da barragem de Petit Saut. Baseado em um mapa
do reservatório (Brasil, ELETRONORTE, s/d [C. 2002]b), o primeiro compartimento
é conectado ao segundo por três passagens com comprimento médio de 1,6 km, o
segundo e terceiro compartimento estão conectados por duas passagens com
comprimento médio de 1,7 km, o terço e quarto compartimentos estão conectados
por duas passagens com comprimento médio de 1,3 km, e os quarto e quinto
compartimentos estão conectados por uma passagem larga (embora indubitavelmente
rasa na divisa entre as bacias) que pode ser considerada como uma passagem de 0
km de comprimento. Supõe-se que as porcentagens de metano dissolvido liberadas
e oxidadas nestes gargalos sejam proporcionais às porcentagens de liberação e
oxidação que aconteceram ao longo deste mesmo comprimento de rio abaixo da barragem
de Petit Saut (baseado nos dados de Galy-Lacaux et al., 1997). A incerteza
neste caso é muito maior do que no caso dos valores para estas porcentagens
calculadas para o canal de adução porque os gargalos curtos estão dentro da
extensão inicial do rio onde um processo mistura estava acontecendo. As
porcentagens usadas (que são todas muito baixas) também presumem que o processo
pára ao término do gargalo, em lugar de continuar ao longo de alguma distância no
próximo compartimento do reservatório. O resultado líquido é que os gargalos,
considerados em conjunto, só emitem 2,1% do metano, enquanto são oxidados 9,2%
e 88,7% são transmitidos até o final do reservatório.
Assim como no caso das turbinas de
Babaquara, há alguma compensação no sistema para incerteza nas porcentagens
liberadas no canal de adução e nos gargalos. Se forem superestimadas as
emissões do canal de adução e/ou dos gargalos, então a emissão nas turbinas da
casa de força principal de Belo Monte serão subestimada. Observa-se que isto só
se aplica aos valores para a porcentagem emitida, não aos valores usados para a
porcentagem de oxidação nestes canais: qualquer erro para cima ou para baixo na
porcentagem oxidada não seria compensado por uma mudança na direção oposta nas
emissões das turbinas.
Em resumo, incertezas múltiplas
existem no cálculo atual. Pesquisa futura, especialmente se for direcionada aos
parâmetros para os quais o modelo indica que o sistema é mais sensível, ajudará
a reduzir estas incertezas. No entanto, o presente cálculo representa a melhor
informação atualmente disponível. Estes resultados fornecem um componente
necessário para a atual discussão dos impactos potenciais destas represas.
IX.
Comparação com Combustíveis Fóssil
A.) Comparações sem descontar
As
emissões anuais de gases de efeito estufa diminuem com tempo, mas ainda se estabilizam
num nível com impacto significativo. A evolução temporal dos impactos de gases
de efeito estufa, com emissões concentradas nos primeiros anos da vida de uma
represa, é uma das diferenças principais entre represas hidrelétricas e geradoras
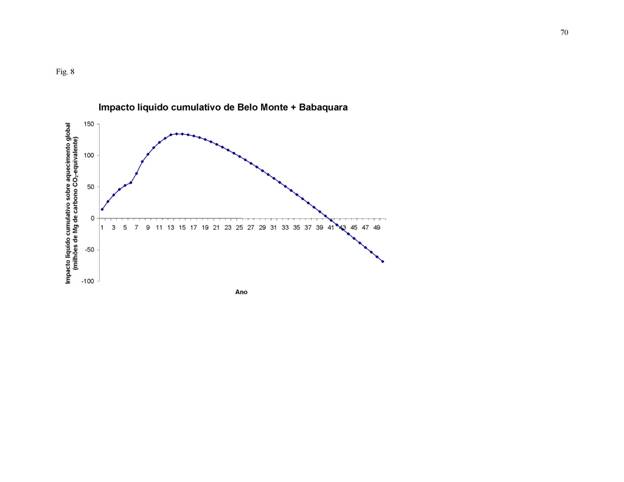
a combustíveis fósseis em termos de efeito estufa (Fearnside, 1997b). Dando
maior peso aos impactos em curto prazo aumenta o impacto das hidrelétricas em
relação as de combustíveis fósseis.
O carbono deslocado de combustível
fóssil pode ser calculado baseado na suposição de que a alternativa é geração a
partir de gás natural. Esta é uma suposição mais razoável do que o
petróleo como referência, já que a expansão atual da capacidade geradora em São
Paulo e em outras partes da rede elétrica no Centro-Sul do Brasil está vindo de
usinas termoelétricas movidas a gás e abastecidas pelo novo gasoduto
Bolívia-Brasil. O gasoduto já existe e não é considerado como parte das
emissões de construção das usinas termoelétricas a gás.
Deslocamento de combustível fóssil é
mostrado na Figura 7 em uma base anual. O complexo começa a ganhar terreno em
compensar pelas suas emissões depois do ano 15. O equilíbrio com emissões de
gases de efeito estufa em uma base cumulativa é mostrado na Figura 8. O
complexo somente terá um saldo positivo em termos de seu impacto no aquecimento
global 41 anos depois do enchimento da primeira represa.
[Figura
7 e 8 aqui]
São apresentadas
médias em longo prazo de emissões líquidas de gases de efeito estufa na Tabela
11 para horizontes de tempo diferentes. Emissões estão separadas naquelas
consideradas sob a rubrica de represas hidrelétricas nos inventários nacionais
que estão sendo preparados pelos países sob a Convenção de Clima (UN-FCCC), e
os outros fluxos que também são parte do impacto e benefício líquido da
represa, incluindo emissões evitadas. Quanto mais longo é o horizonte de tempo,
mais baixo é o impacto médio. Durante os primeiros dez anos o impacto líquido é
4,0 vezes o da alternativa de combustível fóssil. Depois de vinte anos o
impacto líquido ainda é 2,5 vezes maior que o do combustível fóssil, enquanto
para o horizonte de tempo completo de 50 anos o projeto repaga a sua dívida de
aquecimento global (presumindo que é sem juros, isto é, calculada com desconto
zero), com a média de impacto total em longo prazo sendo 70% a da alternativa
de combustível fóssil.
[Tabela
11 aqui]
B.) O efeito do tempo
O papel do tempo é uma parte
essencial no debate sobre represas hidrelétricas e na questão do efeito estufa
em geral. A maioria das decisões, tais como uma decisão para construir uma
hidrelétrica, é baseada em cálculos financeiros de custo/benefício que dão um
valor explícito ao tempo, aplicando uma taxa de desconto a todos os custos e
benefícios futuros. A taxa de desconto é essencialmente o oposto de uma taxa de
juros, como por exemplo, o retorno que um investidor poderia ganhar em uma
caderneta de poupança em um banco. Com uma poupança, quanto mais tempo se
espera, maior a quantia monetária na conta, já que o saldo é multiplicado por
uma porcentagem fixa ao término de cada período de tempo e os juros resultantes
são acrescentados ao saldo para o próximo período. Com uma taxa de desconto, o
valor atribuído a quantidades futuras diminui, em lugar de aumentar, por uma
porcentagem fixa em cada período de tempo. Se um projeto como uma barragem
hidrelétrica produz grandes impactos nos primeiros anos, como o tremendo pico
de emissões de gás de efeito estufa mostrado aqui, enquanto os benefícios pela
substituição de combustível fóssil somente se acumulam em longo prazo, então
qualquer taxa de desconto positiva pesará contra a opção hidrelétrica
(Fearnside, 1997b).
A evolução temporal das emissões de gases de efeito estufa
aumenta mais o impacto da represa quando são contadas as emissões do cimento,
aço e combustível fóssil usados na construção da obra. As emissões de
construção da barragem vêm anos antes de qualquer geração de eletricidade. Uma
análise de “cadeia completa de energia”, ou FENCH, incluiria todas estas
emissões. Porém, as emissões de construção são uma parte relativamente pequena
do impacto total. São mostradas as emissões líquidas anuais descontadas a taxas
de até 3% na Figura 9. Se apenas o equilíbrio instantâneo é considerado, o
complexo substitui por mais carbono equivalente do que emite começando no ano
16, independente da taxa de desconto. Depois disso o complexo começa a pagar a
sua dívida ambiental referente às grandes emissões líquidas dos primeiros 15
anos.
[Figura
9 aqui]
As emissões cumulativas descontadas
chegam a um pico no ano 15, mas não alcançam o ponto de ter um saldo positivo
até pelo menos 41 anos depois que o primeiro reservatório esteja cheio (Figura
10). Aplicar uma taxa de desconto alonga substancialmente o tempo necessário para
alcançar este ponto.
[Figura
10 aqui]
O efeito de taxas de desconto anuais
diferentes é mostrado na Figura 11. Com
desconto zero, o impacto líquido médio representa um ganho anual de 1,4 milhões
de Mg C (a média de 50 anos na Tabela 11), mas o impacto relativo atribuído à
opção hidrelétrica aumenta muito quando o valor tempo é considerado. No caso do
complexo Belo Monte/Babaquara, qualquer taxa de desconto anual superior a 1,5%
resulta ao projeto um impacto maior sobre o efeito estufa do que a alternativa
de combustível fóssil. São mostradas taxas de desconto de até 12%. Embora este autor não defenda o uso de taxas
de desconto tão altas como estas (Fearnside, 2002b,c), um contingente
importante nos
.
[Figura
11 aqui]
Em
termos de efeito estufa, uma série de argumentos fornece uma razão para dar um
valor ao tempo nos cálculos sobre emissões de gases de efeito estufa
(Fearnside, 1995b, 1997b, 2002b,c; Fearnside et al., 2000). O efeito
estufa não é um evento pontual, como uma erupção vulcânica, já que uma mudança
de temperatura seria essencialmente permanente, aumentando as probabilidades de
secas e de outros impactos ambientais. Qualquer adiamento nas emissões de gases
de efeito estufa , e do aumento conseqüente da temperatura, então representa um
ganho das vidas humanas e outras perdas que teriam acontecido caso contrário ao
longo do período do adiamento. Isto dá para o tempo um valor que é independente
de qualquer perspectiva “egoísta” da geração atual. Apesar dos benefícios de
dar valor ao tempo para favorecer decisões que adiam o efeito estufa, chegar a
um acordo político sobre os pesos apropriados para o tempo é extremamente
difícil. O curso de menor resistência nas primeiras rodadas de negociações
sobre o Protocolo de Kyoto foi de usar um horizonte de tempo de 100 anos, sem
descontar ao longo deste período, como o padrão para comparações entre os diferentes
gases de efeito estufa (i.e., o
potencial de aquecimento global de 21 adotado para metano). Se formulações
alternativas são usadas que dão um peso ao tempo, o impacto do complexo Belo
Monte/Babaquara aumentaria, e, mais importante ainda, aumentaria o impacto de
hidrelétricas comparadas a outras possíveis opções para provisão de energia.
O
debate sobre provisão de energia e substituição de combustível fóssil precisa
ir além de cálculos simples de combustível queimado por kWh gerado. No caso de grandes
represas amazônicas, não é necessariamente verdade que, ao deixar de construir
uma barragem, uma quantidade equivalente de combustível fóssil seria queimada
no seu lugar. Isto porque pouco da energia gerada é usada para propósitos essenciais
que seriam de difícil redução, tais como no consumo residencial e indústrias que
atendem o mercado doméstico. Ao invés disso, uma porcentagem significativa e
crescente da energia da rede nacional brasileira é destinada para indústrias
eletrointensivas, tais como as que fabricam o alumínio. O Brasil exporta grandes quantidades de
alumínio barato, e altamente subsidiado (especialmente para o Japão).
O
alumínio que o Brasil exporta é beneficiado usando eletricidade de
hidrelétricas que são construídas com o dinheiro dos contribuintes e
consumidores residenciais brasileiros.
Se menos hidrelétricas fossem construídas, o resultado provável seria diminuir
o subsídio financeiro e ambiental dado ao Mundo como um todo, em lugar de
continuar suprindo energia a uma indústria de exportação de alumínio com base no
aumento de geração de energia a partir de combustíveis fósseis. Companhias de
alumínio que atendem o mercado internacional (distinto do consumo doméstico
brasileiro) teriam que se remover para outro país ou, no final das contas,
teriam que produzir menos alumínio e explorar outros materiais de menor
impacto. O preço do alumínio subiria para refletir o verdadeiro custo ambiental
desta indústria muito esbanjadora, e o consumo global diminuiria a um nível
mais baixo. Acrescentar mais uma usina hidrelétrica à rede nacional apenas posterga
ligeiramente o dia quando o Brasil e o Mundo enfrentarão esta transformação
fundamental. Um dia a contabilidade destes custos ambientais será feita e
considerada antes de tomar decisões, tais como transações para ampliar as
indústrias eletrointensivas no Brasil. A recente onda em transações industriais
com a China, após uma visita presidencial àquele país em 2004, fornece um
exemplo altamente pertinente. Quando são feitos acordos que demandam grandes
quantidades adicionais de eletricidade, então os estudos de impacto ambiental e
o processo de licenciamento para as várias barragens planejadas tendem a se
tornar meros enfeites decorativos para uma série de obras predeterminadas.
X. Conclusões
O complexo hidrelétrica Belo Monte/Babaquara
teria um impacto significativo sobre o efeito estufa, embora a quantidade
grande de energia produzida compensaria eventualmente as emissões iniciais
altas. As
hipóteses usadas aqui indicam que 41 anos seriam necessários para o complexo
chegar a ter um saldo positivo em termos de impacto sobre o aquecimento global no
cálculo mais favorável a hidrelétricas, sem aplicação de nenhuma taxa de
desconto. Apesar de incerteza alta sobre vários parâmetros fundamentais, a
conclusão geral parece ser robusto. Isto
é, que o complexo teria impacto significativo, e que o nível de impacto a longo
prazo, embora muito mais baixo do que nos primeiros anos, seria mantido em
níveis apreciáveis.
A presente análise inclui várias suposições
conservadoras relativo às porcentagens de metano emitidas por caminhos
diferentes. Valores mais altos para estes parâmetros estenderiam ainda mais o
tempo necessário para o complexo ter um saldo positivo em termos de aquecimento
global.
O impacto atribuído a represas é
altamente dependente de qualquer valor dado à evolução temporal das emissões: qualquer taxa de desconto ou
outro mecanismo de preferência temporal aplicado aumentaria mais o impacto
calculado para hidrelétricas em comparação com geração com combustíveis
fósseis. O valor de 41 anos para uma emissão de gases de efeito estufa desta
magnitude é até mesmo significativo a zero desconto. O complexo Belo
Monte/Babaquara não terá um saldo positivo até o final do horizonte de tempo de
50 anos com taxas de desconto anuais superiores de 1,5%.
Os casos de Belo Monte e das outras
barragens do Xingu ilustram a necessidade absoluta de se considerar as
interligações entre projetos diferentes de infra-estrutura e incluir estas
considerações como uma condição prévia para construir ou autorizar quaisquer
dos projetos. Adiar a análise dos projetos mais controversos não é uma solução.
Agradecimentos
O Conselho Nacional de
Desenvolvimento Científico e Tecnológico (CNPq AI 470765/01-1) e o Instituto
Nacional de Pesquisas da Amazônia (INPA PPI 1-3620) contribuíram com apoio
financeiro. Agradeço a Neusa
Hamada, Reinaldo Barbosa, Paulo M.L.A. Graça, Glenn Switkes e ao seu sogro pelos comentários.
Referências
Albritton,
D.L., R.G. Derwent, I.S.A. Isaksen, M. Lal & D.J. Wuebbles. 1995. Trace gas
radiative forcing indices. p. 205-231. In: J.T. Houghton, L.G. Meira Filho, J.
Bruce, Hoesung Lee, B.A. Callander, E. Haites, N. Harris & K. Maskell (eds.),
Climate Change 1994: Radiative Forcing of
Climate Change and an Evaluation of the IPCC IS92 Emission Scenarios. Cambridge University Press, Cambridge, Reino
Unido. 339 p.
Brasil, ANEEL. 2001. Descargas médias de
longo período: Bacia do Amazonas-Rios Tapajós/Amazonas/Iriri/Xingu. http://www.aneel.gov.br/cgrh/atlas/subbac/sub18_f.jpg.
Brasil, ELETROBRÁS & DNAEE.
1997. Instruções para Estudos de Viabilidade de
Aproveitamentos Hidrelétricos.
Centrais Elétricas do Brasil (ELETROBRÁS) &
Departamento Nacional de Água e Energia Elétrica (DNAEE), Brasília, DF, Brasil.
Brasil, ELETRONORTE. 1987a. Esclarecimento Público: Usina Hidrelétrica
Balbina. Modulo 1, Setembro 1987. Centrais Elétricas do Norte do Brasil S.A.
(ELETRONORTE), Brasília, DF, Brasil.
4 p.
Brasil,
ELETRONORTE, 1987b. UHE Balbina:
Enchimento do Reservatório, Considerações Gerais. BAL-39-2735-RE. Centrais Elétricas do
Norte do Brasil S.A. (ELETRONORTE), Brasília, DF, Brasil. 12 p. + anexos.
Brasil,
ELETRONORTE. 2002. Complexo Hidrelétrico Belo Monte: Estudos De
Viabilidade, Relatório Final. Centrais Elétricas do Norte do Brasil S.A. (ELETRONORTE),
Brasília, DF, Brasil. 8 vols.
Brasil,
ELETRONORTE. nd. [C. 1988]. The Altamira
Hydroelectric Complex. Centrais Elétricas do Norte do Brasil S.A. (ELETRONORTE), Brasília, DF, Brasil. 16 p.
Brasil,
ELETRONORTE. nd. [C. 1989]. Altamira.txt.
Centrais
Elétricas do Norte do Brasil S.A. (ELETRONORTE), Brasília, DF, Brasil. 6 p. (disponível de: Faculdade
de Engenharia Mecânica, Universidade Estadual de Campinas-UNICAMP, Campinas,
SP, Brasil).
Brasil, ELETRONORTE. s/d[C. 2002]a. Complexo Hidrelétrico Belo
Monte: Estudo de Impacto Ambiental- E I A. Versão preliminar. Centrais Elétricas do Norte do
Brasil S.A. (ELETRONORTE), Brasília, DF,
Brasil. 6 vols.
Brasil, ELETRONORTE. s/d[C.
2002]b. CHE Belo Monte – Estudos de Viabilidade. Localização geral de obras,
infraestrutura, acessos e rede de distribuição de energia. Ilustração 232, BEL-V 10-100-0024 R-0. Map scale: 1:200,000. Centrais Elétricas do Norte do
Brasil S.A. (ELETRONORTE), Brasília, DF,
Brasil.
Brasil, MME-CCPESE. 2002. Plano Decenal de Expansão 2003-2012: Sumário
Executivo. Ministério das Minas e Energia, Comité Coordinador do
Planejamento da Expansão dos Sistemas Elétricas
(MME-CCPESE), Brasília, DF, Brasil. 75 p.
Brown,
S. & A.E.
da Cruz, P.T. 1996. 100 Barragens Brasileiras: Casos Históricos,
Materiais de Construção, Projeto. Oficina de Texto, São Paulo, SP,
Brasil. 648 p.
de Lima, I.B.T. 2002. Emissão de metano em reservatórios
hidrelétricos amazônicos através de leis de potência. Ph.D. thesis in
nuclear energy, Centro de Energia Nuclear na Agricultura (CENA), Universidade
de São Paulo, Piracicaba, São Paulo, SP, Brasil. 108 p.
de Lima,
I.B.T., R.L. Victoria, E.M.L.M. Novo, B.J. Feigl, M.V.R. Ballester & J.M.
Omero. 2002. Methane, carbon dioxide and nitrous oxide emissions from two
Amazonian reservoirs during high water table. Verhandlungen International
Vereinigung für Limnologie
28(1): 438-442.
de Miranda, E.E.,
J.R. de Miranda & P.F. dos Santos. 1988. Efeitos ecológicos das barragens
do Xingu: Uma avaliação preliminar. p. 83-102 In: L.A.O. Santos & L.M.M. de
Andrade (eds.) As Hidrelétricas do Xingu
e os Povos Indígenas. Comissão Pró-Índio de São Paulo, São Paulo, SP, Brasil. 196 p.
Dones, R. & U. Gantner. 1996. Greenhouse gas
emissions from hydropower full energy chain in
Dumestre, J.F., J. Guezenec, C. Galy-Lacaux, R.
Delmas,
Fearnside, P.M. 1989.
Fearnside,
P.M. 1990. A
Hidrelétrica de Balbina: O Faraonismo Irreversível versus o Meio Ambiente na
Amazônia. Instituto de Antropologia Meio-Ambiente (IAMÁ), São Paulo, SP, Brasil. 63 p.
Fearnside, P.M. 1995a.
Hydroelectric dams in the Brazilian Amazon as sources of 'greenhouse'
gases. Environmental Conservation
22(1): 7-19.
Fearnside, P.M. 1995b. Global warming
response options in
Fearnside, P.M. 1996a. Hydroelectric dams in Brazilian Amazonia:
Response to
Fearnside, P.M. 1996b.
Fearnside, P.M. 1997a. Wood density for estimating forest biomass in
Brazilian Amazonia.
Fearnside,
P.M. 1997b. Greenhouse-gas emissions from Amazonian hydroelectric reservoirs:
The example of
Fearnside, P.M. 2000.
Global warming and tropical land-use change: Greenhouse gas emissions
from biomass burning, decomposition and soils in forest conversion, shifting
cultivation and secondary vegetation. Climatic
Change 46(1-2): 115-158.
Fearnside, P.M. 2001.
Environmental impacts of
Fearnside, P.M. 2002a. Greenhouse
gas emissions from a hydroelectric reservoir (
Fearnside, P.M. 2002b. Time preference in global warming calculations: A
proposal for a unified index. Ecological
Economics 41: 21-31.
Fearnside,
P.M. 2002c. Why a 100-year time horizon should be used for global warming
mitigation calculations. Mitigation and Adaptation Strategies for
Global Change 7(1): 19-30.
Fearnside, P.M. 2004. Greenhouse
gas emissions from hydroelectric dams: Controversies provide a springboard for
rethinking a supposedly “clean” energy source, Climatic Change 66(1-2): 1-8.
Fearnside, P.M. s/d-a.
.
Fearnside,
P.M. s/d-b. Do hydroelectric dams mitigate
global warming? The case of
Fearnside, P.M., D.A. Lashof & P. Moura-Costa. 2000. Accounting for time in mitigating global
warming through land-use change and forestry. Mitigation and Adaptation Strategies for Global Change 5(3):
239-270.
Fearnside,
P.M., N. Leal Filho & F.M. Fernandes. 1993.
Rainforest burning and the global carbon budget: Biomass, combustion
efficiency and charcoal formation in the Brazilian Amazon’. Journal of Geophysical Research
(Atmospheres) 98(D9): 16.733-16.743.
Furch, K. & W.J. Junk.
1992. Nutrient dynamics of submersed decomposing Amazonian herbaceous plant
species Paspalum fasciculatum and Echinochloa polystachya. Revue D’Hydrobiologie Tropicale 25(2):
75-85.
Furch, K. & W.J. Junk.
1997. The chemical compostion, food
value, and decomposition of herbaceous plants, leaves, and leaf litter of
floodplain forests. p. 187-205. In: W.J.
Junk (ed.) The Central Amazon Floodplain
– Ecology of a Pulsing System.
Springer-Verlag,
Gagnon, L. 2002. The
International Rivers Network statement on GHG emissions from reservoirs, a case
of misleading science. International Hydropower Association, Sutton,
Galy-Lacaux, C., R. Delmas, C. Jambert, J.-F.
Dumestre, L. Labroue, S. Richard & P. Gosse. 1997. Gaseous emissions
and oxygen consumption in hydroelectric dams: A case study in French Guyana. Global Biogeochemical Cycles 11(4):
471-483.
Galy-Lacaux, C., R. Delmas, J. Kouadio, S. Richard
& P. Gosse. 1999. Long-term greenhouse gas emissions from hydroelectric
reservoirs in tropical forest regions. Global
Biogeochemical Cycles 13(2): 503-517.
IHA. s/d[C. 2002]. Greenhouse gas emissions from reservoirs. International
Hydropower Association (IHA), Sutton,
Ikusima,
Indriunas, L.
1998. "FHC inaugura obras em viagem ao Pará". Folha de São Paulo.
14 de julho de 1998, p. 1-17.
IRN. 2002. Flooding the Land, Warming the Earth:
Greenhouse Gas Emissions from Dams. International Rivers Network (IRN),
Jordan, C.T. & C. Uhl. 1978. Biomass of a "tierra firme" forest of the
Junk, W.J. & K. Furch.
1991. Nutrient dynamics in Amazonian floodplains: Decomposition of herbaceous
plants in aquatic and terrestrial environments.
Verhandlungen International
Vereinigung für Limnologie 24: 2.080-2.084.
Junk, W.J. & M.T.F.
Piedade. 1997. Plant life in the floodplain with special reference to
herbaceous plants. In: W.J. Junk (ed.) The
Central Amazon Floodplain – Ecology of a Pulsing System. Springer-Verlag,
Junk, W.J., B.A. Robertson, A.J. Darwich &
Klinge, H. 1973. Biomasa y materia orgánica del suelo en el ecosistema de
la pluviselva centro-amazónico. Acta
Científica Venezolana 24: 174-181.
Klinge, H.
& W.A. Rodrigues. 1973. Biomass estimation in a central Amazonian rain forest. Acta Cientifica Venezolana 24: 225-237.
Maceira, M.E.P. & J.M. Damázio. nd. Analysis of the streamflow record extension for
the
Martius, C., P.M. Fearnside, A.G.
Bandeira & R. Wassmann. 1996. Deforestation and methane release from
termites in
Martius,
C., R. Wassmann, U. Thein, A.G. Bandeira, H. Rennenberg, W. Junk & W.
Seiler. 1993. Methane emission from wood-feeding termites in
McCulloch, M. & J. Vadgama. 2003. Life-cycle
evaluation of GHG emissions and land change related to selected power
generation options in
Melack,
J. & B.R. Forsberg. 2001. Biogeochemistry of Amazon floodplain lakes and
associated watersheds. p. 235-274 In:
M.E. McClain, R.L. Victoria & J.E. Richey (eds.) The Biogeochemistry of the
Melack, J.M. & L.L. Hess.
2004. Remote sensing of wetlands on a global
scale. SILnews, No. 42: 1-5. http://www.limnology.org/news/silnews42.pdf
Mori,
S. A. & P. Becker. 1991. Flooding affects survival of Lecythidaceae in
terra firme forest near
Paiva, M.P. 1977. The
Environmental Impact of Man‑Made Lakes in the Amazonian Region of
Peisajovich, A., A. Chamberland & L. Gagnon. 1996.
Greenhouse gases from full energy cycle of northern hydro-electricity
(preliminary assessment of production and transportation). In: Assessment of Greenhouse Gas Emissions
from the Full Energy Chain for Hydropower, Nuclear Power and Other Energy
Sources. Papers Presented at an IAEA Advisory Group Meeting Jointly Organized
by Hydro-Québec and the International Atomic Energy Agency, Hydro-Québec
Headquarters,
Pinto, L.F. 2002. Hidrelétricas
na Amazônia: Predestinação, Fatalidade ou Engodo? Edição Jornal Pessoal,
Belém, Pará, Brasil. 124 p.
Potter, C.S., E.A. Davidson & L.V.
Verchot. 1996.
Estimation of global biogeochemical controls and seasonality on soil methane
consumption. Chemosphere 32: 2.219-2.246.
Ramaswamy, V. & 40 others.
2001. Radiative forcing of climate change.
p. 349-416 In: Houghton, J.T., Ding,
Y., Griggs, D.G., Noguer, M., Van der Linden, R.J. & Xiausu, D. (eds.). Climate Change 2001: The Scientific Basis.
Revilla Cardenas, J.D.
1987. Relatório: Levantamento e Análise da Fitomassa da UHE de Kararaô, Rio
Xingú. Instituto Nacional de Pesquisas da Amazônia (INPA), Manaus, Amazonas, Brasil.
Revilla Cardenas, J.D.
1988. Relatório: Levantamento e Análise da Fitomassa da UHE de Babaquara, Rio
Xingú. Instituto Nacional de Pesquisas da Amazônia (INPA), Manaus, Amazonas,
Brasil.
Rosa, L.P., M.A. dos Santos, J.G. Tundisi & B.M. Sikar.
1997. Measurements of greenhouse gas emissions
in Samuel, Tucuruí and Balbina Dams. p.
41-55 In: L.P. Rosa & M.A. dos
Rosa, L.P., R. Schaeffer & M.A dos Santos. 1996. Are
hydroelectric dams in the Brazilian Amazon significant sources of 'greenhouse'
gases? Environmental
Conservation 23(2): 2-6.
Rosa, L.P., B.M. Sikar, M.A. dos Santos & E. M.
Sikar. 2002. Emissões de dióxido de
carbono e de methano pelos reservatórios hidrelétricos brasileiros. Primeiro
Inventário Brasileiro de Emissões Antrópicos de Gases de Efeito Estufa.
Relatórios de Referência. Instituto Alberto Luiz Coimbra de Pós-Graduação e
Pesquisa em Engenharia (COPPE). Ministério da Ciência e Tecnologia (MCT),
Brasília, DF, Brasil. 119 p. http://www.mct.gov.br/clima/comunic_old/pdf/metano_p.pdf
Rosenqvest, A., B.R. Forsberg,
T.P. Pimentel, Y.A. Rausch & J.E. Richey. 2002. The use of spacebourne radar data to model
inundation patterns and trace gas emissions in the Central Amazon
floodplain. International Journal of Remote Sensing 7: 1303-1328.
Schimel, D. & 75 others. 1996. Radiative forcing
of climate change. p. 65-131. In: J.T. Houghton, L.G. Meira Filho, B.A. Callander,
N. Harris, A. Kattenberg & K. Maskell (eds.) Climate Change 1995: The
Science of Climate Change.
Seva,
O. 1990. Works on the great bend of the
Trumbore,
S.E., G. Bonani & W. Wölfli. 1990. The rates of carbon cycling in several
soils from AMS 14C measurements of fractionated soil organic matter.
p. 407-414 In: A.F. Bouman (ed.) Soils and the Greenhouse Effect. John Wiley
& Sons,
UN-FCCC.
2004. Executive Board of the Clean Development Mechanism Seventeenth Meeting
Report. CDM-EB-17,
Van de Vate, J.F. 1995. The IAEA
investigations into studies on comparative assessment of FENCH emissions of
GHGs of different energy sources: An update. Assessment of Greenhouse Gas Emission from the Full Energy Chain for
Nuclear Power and Other Energy Sources. IAEA,
Verchot, L.V., E.A. Davidson, J.H. Cattânio, I.L. Akerman, H.E. Erickson, & M. Keller.
Vieira, I. 1982. Aspectos Sinecológicos da Ictiofauna de Curuá-Úna, Represa
Hidroelétrica da Amazônia Brasileira. “Livre docencia” thesis in biology,
Universidade Federal de Juiz de Fora, Juiz de Fora, Minas Gerais, Brasil. 107 p.
Wassmann, R. & C. Martius.
1997. Methane emissions from the Amazon floodplain. p.137-143. In: W.J. Junk (ed.) The Central Amazon Floodplain – Ecology of a Pulsing System. Springer-Verlag,
LEGENDAS
DAS FIGURAS
Figura
1. A.) Babaquara
(Altamira) Reservatório; B.) Reservatórios de Belo Monte da Calha e dos Canais.
Fontes: Babaquara: Brasil, ELETRONORTE, s/d[C. 1988]; Belo Monte: Brasil,
ELETRONORTE, s/d[C. 2002]a.
Figura.
2. Concentração de metano
às 30 m de profundidade contra carbono decomposto anaerobicamente. Dados de
concentração aos 30 m são de Petit Saut (Galy-Lacaux et al., 1999) que é de Tucuruí (J.G. Tundisi, citado por Rosa et al.,
1997, pág. 43).
Figura
3. Ebuliação e emissões de
difusão contra concentração de metano predita aos 30 m de profundidade. Dados
de emissões são de Petit Saut (Galy-Lacaux et
al., 1999). A.) Ebuliação para locais 0-3 m de profundidade; B.) Emissões
de ebulição para 4-6 m de profundidade; C.) Emissões de ebulição para 7-8 m de
profundidade; D.) Emissões de difusão para todas as profundidades.
Figura.
4. Fontes de carbono
decomposto anaerobicamente: A.) Babaquara (Altamira) reservatório; B.) Belo
Monte Reservatório da Calha; C.) Belo Monte Reservatório dos Canais.
Figura
5. Metano calculado a 30
m de profundidade: A.) Reservatório de
Babaquara (Altamira); B.) Belo Monte Reservatório da Calha; C.) Belo Monte Reservatório
dos Canais.
Figura
6. Emissões por caminho
para o complexo Belo Monte/Babaquara (Altamira). O complexo começa a reembolsar
sua dívida de emissões de gás de efeito estufa após o 15º ano depois de encher
o primeiro reservatório.
Figura
7. Emissões anuais e
substituição de combustível fóssil.
Figura
8. Impacto de aquecimento
globallíquido cumulativo do complexo Belo Monte/Babaquara (Altamira) (sem
descontar). O complexo só consegue um saldo positívo depois de 39 anos.
Figura
9. Emissões líquidas
anuais descontadas. Em uma base anual, o complexo começa a reembolsar suas
emissões iniciais depois do ano 15, independente de taxa de desconto.
Figura
10. Emissões cumulativas
descontadas. Descontando estende o tempo precisado para o complexo para
conseguir um saldo positivo em termos de seu impacto acumulado.
Figura
11. Efeito de taxa de
desconto em emissões líquidas anuais médias ao longo de um horizonte de tempo
de 50 anos. Se for usado uma taxa de desconto anual de 1,8% ou mais, o complexo
tem um impacto maior sobre o efeito estufa do que a alternativa de combustível
fóssil.
LISTA DAS TABELAS
Tabela 1: Características técnicas das barragens de Belo Monte (Kararaô)
e Babaquara (Altamira).
Tabela 2: Relação entre as concentrações a diferentes profundidades e a
concentração de CH4 aos 30 m de profundidade.
Tabela 3: Relação entre as emissões de ebulição e de difusão e a
concentração de CH4 aos 30 m de profundidade.
Tabela 4: Parâmetros para a emissão gases da biomassa acima da água no
reservatório de Babaquara.
Tabela 5: Área e biomassa de vegetação em Belo Monte e Babaquara .
Tabela 6: Fluxo de metano evitado pela perda de floresta em Babaquara.
Tabela 7: Emissão de óxido nitroso da perda de floresta em Babaquara.
Tabela 8: Aço usado na construção de Belo
Monte e Babaquara.
Tabela 9: Cimento usado na construção de Belo
Monte e Babaquara.
Tabela 10: Emissões de gás de efeito estufa da construção da barragem e
da linha de transmissão.
Tabela 11: Médias a longo prazo de emissão líquida de gás de efeito
estufa para o complexo Belo Monte/Babaquara
LEGENDAS
DAS FIGURAS
Figura
1. A.) Babaquara
(Altamira) Reservatório; B.) Reservatórios de Belo Monte da Calha e dos Canais.
Fontes: Babaquara: Brasil, ELETRONORTE, s/d[C. 1988]; Belo Monte: Brasil,
ELETRONORTE, s/d[C. 2002]a.
Figura.
2. Concentração de metano
às 30 m de profundidade contra carbono decomposto anaerobicamente. Dados de
concentração aos 30 m são de Petit Saut (Galy-Lacaux et al., 1999) que é de Tucuruí (J.G. Tundisi, citado por Rosa et al.,
1997, pág. 43).
Figura
3. Ebuliação e emissões de
difusão contra concentração de metano predita aos 30 m de profundidade. Dados
de emissões são de Petit Saut (Galy-Lacaux et
al., 1999). A.) Ebuliação para locais 0-3 m de profundidade; B.) Emissões
de ebulição para 4-6 m de profundidade; C.) Emissões de ebulição para 7-8 m de
profundidade; D.) Emissões de difusão para todas as profundidades.
Figura.
4. Fontes de carbono
decomposto anaerobicamente: A.) Babaquara (Altamira) reservatório; B.) Belo
Monte Reservatório da Calha; C.) Belo Monte Reservatório dos Canais.
Figura
5. Metano calculado a 30
m de profundidade: A.) Reservatório de
Babaquara (Altamira); B.) Belo Monte Reservatório da Calha; C.) Belo Monte
Reservatório dos Canais.
Figura
6. Emissões por caminho
para o complexo Belo Monte/Babaquara (Altamira). O complexo começa a reembolsar
sua dívida de emissões de gás de efeito estufa após o 15º ano depois de encher
o primeiro reservatório.
Figura
7. Emissões anuais e substituição
de combustível fóssil.
Figura
8. Impacto de aquecimento
globallíquido cumulativo do complexo Belo Monte/Babaquara (Altamira) (sem
descontar). O complexo só consegue um saldo positívo depois de 41 anos.
Figura
9. Emissões líquidas
anuais descontadas. Em uma base anual, o complexo começa a reembolsar suas
emissões iniciais depois do ano 15, independente de taxa de desconto.
Figura
10. Emissões cumulativas
descontadas. Descontando estende o tempo precisado para o complexo para
conseguir um saldo positivo em termos de seu impacto acumulado.
Figura
11. Efeito de taxa de
desconto em emissões líquidas anuais médias ao longo de um horizonte de tempo
de 50 anos. Se for usado uma taxa de desconto anual de 1,5% ou mais, o complexo
tem um impacto maior sobre o efeito estufa do que a alternativa de combustível
fóssil.
LISTA DAS TABELAS
Tabela 1: Características técnicas das barragens de Belo Monte (Kararaô)
e Babaquara (Altamira).
Tabela 2: Relação entre as concentrações a diferentes profundidades e a
concentração de CH4 aos 30 m de profundidade.
Tabela 3: Relação entre as emissões de ebulição e de difusão e a
concentração de CH4 aos 30 m de profundidade.
Tabela 4: Parâmetros para a emissão gases da biomassa acima da água no
reservatório de Babaquara.
Tabela 5: Área e biomassa de vegetação em Belo Monte e Babaquara .
Tabela 6: Fluxo de metano evitado pela perda de floresta em Babaquara.
Tabela 7: Emissão de óxido nitroso da perda de floresta em Babaquara.
Tabela 8: Aço usado na construção de Belo
Monte e Babaquara.
Tabela 9: Cimento usado na construção de Belo
Monte e Babaquara.
Tabela 10: Emissões de gás de efeito estufa da construção da barragem e
da linha de transmissão.
Tabela 11: Médias a longo prazo de emissão líquida de gás de efeito
estufa para o complexo Belo Monte/Babaquara
|
Tabela 1: Características Técnicas das Represas de
Belo Monte (Kararaô) e Babaquara (Altamira) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Item |
Unidades |
Belo Monte
(Kararaô) |
Total |
Babaquara
(Altamira) |
Nota |
||
|
|
|
Reservatório da
Calha |
Reservatório
dos canais |
Belo Monte |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Área do
reservatório no nível máximo operacional normal |
km2 |
333 |
107 |
440 |
6,140 |
|
|
|
Área do
reservatório no nível mínimo operacional normal |
km2 |
333 |
102 |
438 |
2,560 |
|
|
|
Área de
deplecionamento |
km2 |
0 |
5 |
5 |
3,580 |
|
|
|
Variação do
nível d’água |
m |
0 |
1 |
|
23 |
|
|
|
Volume no nível
máximo operacional normal |
Bilhão de m3
|
2.07 |
1.89 |
3.96 |
143.5 |
|
|
|
Volume no nível
mínimo operacional normal |
Bilhão de m3
|
2.07 |
1.79 |
3.86 |
47.16 |
|
|
|
Volume de
armazenamento vivo |
Bilhão de m3
|
0 |
0.11 |
0.11 |
96.34 |
|
|
|
Profundidade
média |
m |
6.2 |
17.7 |
9.0 |
23.4 |
|
|
|
Tempo de
residência média |
dias |
3.1 |
2.8 |
5.8 |
211.6 |
(a) |
|
|
Comprimento do
reservatório |
km |
60 |
87 |
147 |
564 |
|
|
|
Comprimento do
perímetro da margem |
km |
361 |
268 |
629 |
2,413 |
(b) |
|
|
Número de
turbinas |
Número |
7 |
20 |
27 |
18 |
|
|
|
Produção de
máximo por turbina |
MW |
25.9 |
550 |
-- |
348.6 |
|
|
|
Capacidade
instalada |
MW |
181.3 |
11,000 |
11,181.3 |
6,274 |
|
|
|
Consumo de água
por turbina |
m3/s
|
253 |
695 |
-- |
672 |
|
|
|
Consumo de água
total |
m3/s
|
1,771 |
13,900 |
15,671 |
12,096 |
|
|
|
Vazão
médio |
m3/s
|
|
|
7,851 |
7,851 |
(c) |
|
|
|
|
|
|
|
|
|
|
|
Elevações |
|
|
|
|
|
|
|
|
Nível máximo
operacional normal |
m sobre o mar |
97 |
97 |
-- |
165 |
|
|
|
Nível mínimo
operacional normal |
m sobre o mar |
97 |
96 |
-- |
142 |
(d) |
|
|
Nivel do
vertedouro |
m sobre o mar |
76 |
79.52 |
-- |
145 |
(e) |
|
|
Nível do canal
de adução |
m sobre o mar |
-- |
84 |
-- |
-- |
|
|
|
Eixo da entrada
das turbinas |
m sobre o mar |
80 |
65 |
-- |
116.5 |
|
|
|
|
|
|
|
|
|
|
|
|
Outros
parâmetros |
|
|
|
|
|
|
|
|
Área de
drenagem |
km2 |
|
|
447,719 |
|
|
|
|
Evaporação
anual |
mm |
|
|
1,575 |
|
|
|
|
Precipitação
anual |
mm |
|
|
1,891 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Localização |
Latitude |
03o 26 ' S |
3o 7
' 35 " S |
3o
18 ' 0 " S |
|||
|
|
Longitude |
51o 56 ' O |
51o
46 ' 30 " O |
52o
12'30"O |
|||
|
Notas |
|
|
|
|
|
|
|
|
(a) Presume que toda a água é usada pela
casa de força principal em Belo Monte. |
|
|
|||||
|
(b) Presume-se que Babaquara tem a mesma
a relação entre o perímetro da margem e o comprimento que em Belo Monte. |
|||||||
|
(c) Vazão é a média para 1931-2000
calculada no EIA para Belo Monte. Um vazão “sintético" mais alto "
de 8.041 m3/s foi calculado por Maceira & Damázio (s/d) para
Babaquara. |
|
||||||
|
(d) O Reservatório dos Canais terá um
manejo de água incomum, com o nível mantido em 96 m durante a estação de alto
fluxo e 97 m durante a estação de baixo fluxo (Brasil, ELETRONORTE, 2002). |
|
||||||
|
(e) Solteira do
vertedouro de Babaquara presumida a ser
20 m abaixo do nível operacional normal. |
|
||||||
|
Tabela
2: Razão das concentrações de CH4 em diferentes profundidades para
a concentração aos 30 m de profundidade |
|||
|
|
|
|
|
|
Gama de profundidade (m) |
Idade = 12 meses(a) |
Idade 12,1-36 meses(b) |
Idade > 36 meses (c) |
|
|
|
|
|
|
0 – 0,9 |
0,33 |
0 |
0 |
|
1 – 1,9 |
0,50 |
0 |
0 |
|
2 – 4,9 |
0,75 |
0 |
0 |
|
5 – 9,9 |
0,83 |
0 |
0,34 |
|
10 – 14,9 |
0,67 |
0 |
0,63 |
|
15 – 19,9 |
0,75 |
0,33 |
0,71 |
|
20 – 24,9 |
0,83 |
0,50 |
0,79 |
|
25 – 29,9 |
0,92 |
0,83 |
0,89 |
|
30 – 30,0 |
1,00 |
1,00 |
1,00 |
|
≥ 31 |
(d) |
(d) |
(d) |
|
|
|
|
|
|
(a). Dados do reservatório de Samue l,5 meses depois de encher (J.G. Tundisi, citado por Rosa et al., 1997, pág. 43). |
|||
|
(b) Dados de Petit Saut (Galy-Lacaux et al., 1999). |
|||
|
(c) Dados de Tucurui 44 meses depois de encher (J.G. Tundisi, citado por Rosa et al., 1997, pág. 43). |
|||
|
(D) Y = 1 + (0,0165 (X - 30)) onde: Y = Razão entre a concentração de CH4 e a concentração aos 30 m de profundidade X = Profundidade debaixo da superfície (m) |
|||
|
Tabela 3:
Emissões ebulição e de difusão de concentração de CH4 aos 30 m de
profundidade(a) |
||||
|
Caminho de
emissão |
Gama de
profundidade (m) |
Gama de
concentração de CH4 aos 30 m de profundidade (mg/litro) |
Declive |
Intercepte |
|
|
|
|
|
|
|
Ebulição |
0-3 m |
0-9,2 |
47,572 |
-54,214 |
|
|
|
9,3-1,,6 |
64,979 |
-216,344 |
|
|
|
≥ 17,7 |
23,562 |
516,453 |
|
|
|
|
|
|
|
Ebulição |
4-6 m
|
0-9,2 |
31,284 |
-77,499 |
|
|
|
9,3-17,6 |
35,738 |
-118,989 |
|
|
|
≥ 17,7 |
12,959 |
284,049 |
|
|
|
|
|
|
|
Ebulição |
7-8 m
|
|
|
|
|
|
0-4.5 |
0 |
0 |
|
|
|
|
4,6-9,2 |
2,468 |
43,680 |
|
|
|
9,3-17,6 |
11,139 |
-37,087 |
|
|
|
≥ 17,7 |
4,039 |
88,535 |
|
|
|
|
|
|
|
Difusão |
Todas as
profundidades |
0-9,2 |
11,909 |
-35,860 |
|
|
|
9,3-17,6 |
17,917 |
-91,822 |
|
|
|
≥ 17,7 |
1,895 |
191,656 |
|
|
|
|
|
|
|
(a) Y = m X + b
onde: Y =
Emissão de CH4 (mg/m2/dia) X =
Concentração de CH4 aos 30 m de profundidade (mg/litro) m = Declive b = Intercepte |
||||
|
Tabela 4: Parâmetros para a emissão gases da
biomassa acima da água no reservatório de Babaquara |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Parâmetro |
|
|
|
Valor |
Unidades |
Fonte |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fração acima do
solo |
|
|
|
0,759 |
|
Fearnside
1997b, pág. 337 |
|
|
|
|
|
|
|||
|
Profundidade
médio de zona de água de superfície |
|
1 |
metro |
Suposição,
baseado em deterioração de madeira comercial, |
|
|
|
|
|||||||
|
Taxa de decomposição de folhas na zona
sazonalmente inundada |
|
-0,5 |
Fração/ano |
Suposição. |
|
|
|||||||||
|
Taxa de
decomposição acima d’água (0-4 anos) |
|
|
-0,1680 |
Fração/ano |
Presumido mesmo
como floresta derrubada (Fearnside, 1996b, pág,, 611)(*) |
|
|
|
|||||||
|
Taxa de
decomposição acima d’água (5-7 anos) |
|
|
-0,1841 |
Fração/ano |
Presumido mesmo
como floresta derrubada (Fearnside, 1996b, pág, 611) |
|
|
|
|||||||
|
Taxa de
decomposição acima d’água (8-10 anos) |
|
-0,0848 |
Fração/ano |
Presumido mesmo
como floresta derrubada (Fearnside, 1996b, pág. 611) |
|
|
|
||||||||
|
Taxa de
decomposição acima d’água (>10 anos) |
|
-0,0987 |
Fração/ano |
Presumido mesmo
como floresta derrubada (Fearnside, 1996b, pág, 611) |
|
|
|
||||||||
|
Conteúdo de
carbono de madeira |
|
|
0,50 |
|
Fearnside
et al., 1993 |
|
|
|
|
|
|
||||
|
Biomassa total
médio de floresta a Babaquara |
244 |
Mg/ha |
Revilla Cardenas
(1988) para biomassa acima do solo; Fração acima do
solo como acima. |
|
|||||||||||
|
Profundidade de água médio ao nível
mínimo operacional normal |
|
18,4 |
metros |
A 142 m sobre o
mar |
|
|
|
|
|
|
|
||||
|
Profundidade de
água médio ao nível operacional normal |
23.4 |
metros |
A 165 m sobre o
mar |
|
|
|
|
|
|
|
|||||
|
Biomassa
inicial presente: folhas |
|
|
4.1 |
Mg/ha |
Calculado de
biomassa total e de Fearnside (1995a, pág. 12), |
13.77 |
De
Revilla-Cardenas, 1988, pp. 75 & 77 |
||||||||
|
Biomassa
inicial presente: madeira acima d’água |
|
138,8 |
Mg/ha |
Calculado de
biomassa total e de Fearnside (1995a, pág. 12), |
|
|
|
|
|||||||
|
Biomassa
inicial presente: debaixo do solo |
|
58,8 |
Mg/ha |
Calculado de
biomassa total e de Fearnside (1995a, pág. 12), |
|
|
|
|
|||||||
|
Liberação de
metano por térmitas em floresta |
|
0,687 |
kg
CH4/ha/ano |
Martius et al,, 1996, pág. 527 |
|
|
|
|
|
|
|||||
|
Liberação de metano por térmitas em
biomassa acima d’água por Mg C se deteriorado por térmitas |
0,0023 |
Mg CH4
|
Martius et al., 1993 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Por cento de decomposição mediado por
térmitas acima do nível d’água máximo operacional normal |
4,23 |
% |
Martius
et al. 1996, pág. 527 para biomassa
derrubada |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Por cento de decomposição mediado por
térmitas abaixo da linha d’água do nível máximo operacional normal |
0 |
% |
Baseado em Walker et al., 1999. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Área total do
reservatório ao nível operacional normal |
6.140 |
km2 |
|
|
|
|
|
|
|
|
|
||||
|
Área do leito
fluvial |
|
|
|
136 |
km2 |
Revilla-Cardenas,
1988, pág. 87 |
|
|
|
|
|
|
|||
|
Área desmatada
antes de inundar (zona de inundação permanente) |
0 |
km2 |
|
|
|
|
|
|
|
|
|
||||
|
Área total de
floresta inundada |
|
|
6,004 |
km2 |
Calculado por
diferença |
|
|
|
|
|
|
||||
|
Área de
floresta original na zona de inundação permanente |
2,424 |
km2 |
Área da zona,
menos o leito fluvial e a área previamente desmatada |
|
|
|
|
||||||||
|
Área de
floresta original de zona de deplecionamento |
|
3,580 |
km2 |
Calculado por
diferença de área de floresta de total |
|
|
|
|
|||||||
|
Taxa de quebra
de troncos na altura da linha d’água para árvores > 25 cm DAP |
0,063 |
Fração do
estoque original /ano |
Baseado em Walker
et al., 1999, pág. 245 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Taxa de troncos
que quebram na linha de água para árvores < 25 cm DAP |
0,113 |
Fração do
estoque original /ano |
Baseado em Walker
et al., 1999, pág. 245 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Taxa de queda
de galhos (e presumida queda de troncos acima do primeiro galho) |
0,094 |
Fração do
estoque original /ano |
Baseado em Walker
et al., 1999, pág. 245 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Por cento da
biomassa acima do solo de madeira viva em galhos e tronco acima do primeiro
galho |
30,2 |
% |
Fearnside,
1995a, pág. 12 baseado em Klinge & Rodrigues, 1973 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Por cento da
biomassa de madeira acima do solo em troncos |
69,8 |
% |
Fearnside,
1995a, pág. 12 baseado em Klinge & Rodrigues, 1973 |
|
|
|
|||||||||
|
Por cento de
biomassa de tronco > 25 cm DAP |
|
66,0 |
% |
Calculado
abaixo |
|
|
|
|
|
|
|
||||
|
10-25 cm DAP
como por cento de biomassa de fuste total em árvores
vivos > 10 cm DAP |
22 |
% |
Brown &
Lugo, 1992, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0-10 cm DAP
como por cento de biomassa vivo total acima do solo |
12 |
% |
Jordan &
Uhl, 1978, |
|
|
|
|
|
|||||||
|
Bole como por
cento de Biomassa de sobre-chão ao vivo total em árvores ao
vivo > 10 cm DAP |
57,47 |
% |
Baseado em
fator de expansão de biomassa de 1,74 para bole biomassa >
190 Mg/ha em árvores ao vivo > 10 cm DAP (Brown e Lugo, 1992). |
|
|
||||||||||
|
|
|
|
|
||||||||||||
|
Biomassa viva
acima do solo < 10 cm DAP |
|
22,2 |
Mg/ha |
Calculado a
partir de informações acima . |
|
|
|
|
|
|
|||||
|
Galhos como
porcentatem de biomassa de fuste viva |
|
51,4 |
% |
Baseado em
Brown & Lugo, 1992 |
|
|
|
|
|
|
|||||
|
Biomassa de filial |
|
|
|
55,9 |
Mg/ha |
Calculado a
partir de informações acima |
|
|
|
|
|
|
|||
|
Biomassa acima
do solo de floresta |
|
185,3 |
Mg/ha |
Calculado de
total e fração acima do solo |
|
|
|
|
|||||||
|
Sobre-chão
Biomassa de madeira ao vivo |
|
|
155,5 |
Mg/ha |
Total-folhas-morto
|
|
|
|
|
|
|
|
|||
|
Sobre-chão
Biomassa de madeira morto |
|
25,6 |
Mg/ha |
Klinge, 1973,
pág. 179 |
|
|
|
|
|
|
|
||||
|
Biomassa de
bole ao vivo |
|
|
|
108,6 |
Mg/ha |
Aporcionamento
baseado em Brown & Lugo, 1992 |
|
|
|
|
|
||||
|
Biomassa de
fuste vivo 10-25 cm DAP |
|
23,9 |
Mg/ha |
Aporcionamento
baseado em Brown & Lugo, 1992 |
|
|
|
|
|
||||||
|
Biomassa de
fuste vivo < 10 cm DAP |
|
|
13,0 |
Mg/ha |
Jordan &
Uhl,1978 |
|
|
|
|
|
|
||||
|
Biomassa de
fuste vivo 0-25 cm DAP |
|
|
36,9 |
Mg/ha |
Somado de acima
|
|
|
|
|
|
|
|
|||
|
Biomassa de
fuste vivo > 25 cm DAP |
|
|
71,7 |
Mg/ha |
Partioning
baseado em Brown & Lugo, 1992 |
|
|
|
|
|
|||||
|
Biomassa de
fuste vivo: acima da linha d’água |
|
96,4 |
Mg/ha |
Distribuição
vertical interpolou de Klinge & Rodrigues, 1973, |
|
|
|
||||||||
|
Biomassa de
fuste vivo: 0-25 cm DAP: acima da linha d’água |
32,8 |
Mg/ha |
Distribuição
vertical interpolou de Klinge & Rodrigues, 1973, |
|
|
|
|||||||||
|
Biomassa de
fuste vivo: > 25 cm DAP: acima da linha d’água |
63,6 |
Mg/ha |
Distribuição
vertical interpolou de Klinge & Rodrigues, 1973, |
|
|
|
|||||||||
|
Fração das
árvores que flutuam |
|
|
0,4 |
Fração |
Richard Bruce,
comunicação pessoal, 1993; veja Fearnside, 1997a, pág., 61 |
|
|
||||||||
|
Fração de filiais originais em árvores restantes
que caem por ano |
0,094 |
Fração |
Calculado de Walker et al.,
1999. |
|
|
|
|
|
|||||||
|
Fração médio de
área de drawdown de ano expôs |
0,5 |
Fração |
Estimativa
aproximada baseado no nivel do reservatório em 2000 em Balbina. |
|
|
|
|
||||||||
|
Tabela 5: Área e Biomassa de vegetação ao Belo
Monte e Babaquara(a) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
BABAQUARA |
|
|
BELO MONTE |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Área (km2)
|
Por cento |
Biomassa acima do solo(b)
(Mg/ha peso
seco) |
|
Área (km2)
|
Por cento |
Biomassa acima do solo(b)
(Mg/ha peso
seco) |
|
|||||||||||
|
|
Tipo de
vegetação |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Vegetação não
inundada |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Floresta aberta
de terra firme [floresta
aberta mista (FA)+ floresta aberta
submontana (FS)] |
3.565,3 |
58,0 |
175,2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Floresta aberta
de terra firme sobre revelo
acidentado |
|
|
|
|
205,7 |
46,7 |
125,27 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Floresta aberta
de terra firme sobre revelo
ondulado |
|
|
|
|
11,9 |
2,7 |
201,9 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Floresta
secundária latifoliada |
10.9 |
0.2 |
20.0 |
(c) |
11,0 |
2,5 |
20,0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Vegetação
inundada |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Floresta densa
ciliar estacionalmente inundável ou
Floresta Densa Ciliar (FC) |
2.421,9 |
39,3 |
201,2 |
|
191,5 |
43,6 |
121,2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Floresta Aberta
ciliar estacionalmente submersa
(Formações pioneiras aluviais
campestres) |
5,6 |
0,1 |
60,0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Nenhuma
vegetação (canal de rio) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Áreas sem
cobertura vegetal |
136,3 |
2,4 |
0,0 |
|
20,0 |
4,5 |
0,0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Totais |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Total de
vegetação não inundada |
3.576,3 |
58,2 |
|
|
228,5 |
51,9 |
|
|
|||||||||||||
|
|
Total de
vegetação inundada |
2.427,5 |
39,4 |
|
|
191,5 |
43,6 |
|
|
|||||||||||||
|
|
Vegetação
total |
|
6.003,7 |
97,6 |
185,3 |
|
420,0 |
95,5 |
122,8 |
|
||||||||||||
|
|
Reservatório
total |
|
6.140,0 |
100,0 |
|
|
440,0 |
100,0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(a) Dados de
Revilla Cardenas (1987, p.55; 1988, p.87), com áreas ajustadas em proporção à
estimativa de área de reservatório atual (6.140 km2 para Babaqura;
440 km2 para Belo Monte). |
|
|||||||||||||||||||||
|
(b) Valores
incluem Biomassa morto (liteira e madeira morta), cipós, e o tapete de
raizes. |
|
|
|
|
||||||||||||||||||
|
(c) Valor para
biomassa de floresta secundária acima do solo é aquele usado por Revilla
Cardenas (1988) para Babaquara, baseado em dados de Tucuruí. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Tabela 6: Fluxo evitado de metano da perda de
floresta em Babaquara |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Item |
|
|
Valor |
Unidades |
Fonte |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
ABSORÇÃO PELO SOLO EM FLORESTA NÃO INUNDADA |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
CH4
anual médio suprem com gás absorção |
-3,8 |
kg
CH4/ha/ano |
Potter et al.. (1996) de 22 estudos |
|
|
|
|
|
||||||||||||||||||||||||
|
de não inundada
arborize terra |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Área total de
floresta inundada por reservatório |
6.004 |
km2 |
Baseado em
6.140 área de reservatório de km2 e streambed de Revilla Cardenas, 1988, p.87, |
|
||||||||||||||||||||||||||||
|
Área de floresta
ribeirinha inundada por reservatório |
2.427 |
km2 |
Revilla
Cardenas, 1988, pág. 87 |
|
|
|
|
|||||||||||||||||||||||||
|
Área de
floresta de firme de terra inundada por reservatório |
3.576 |
km2 |
Calculado por
diferença |
|
|
|
|
|
|
|||||||||||||||||||||||
|
Fração de ano
que floresta ribeirinha inundou naturalmente |
0.17 |
Fração |
presumido ser 2
meses, em média |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Absorção por ha
por ano em floresta ribeirinha |
-3,17 |
kg
CH4/ha/ano |
Proporcional
cronometrar não inundada |
|
|
|
||||||||||||||||||||||||||
|
Absorção por
ano em floresta ribeirinha |
-768,70 |
Mg
CH4/ano |
Absorção por ha
área de X de floresta ribeirinha |
|
|
|
|
|||||||||||||||||||||||||
|
Absorção por
ano em floresta de firme de terra |
-1.358,98 |
Mg
CH4/ano |
Absorção
por ha área de X de floresta de firme de terra |
|
|
|
|
|||||||||||||||||||||||||
|
Absorção
total por ano |
|
-2.127,68 |
Mg
CH4/ano |
Some
através de tipo de floresta |
|
|
|
|
||||||||||||||||||||||||
|
Potencial de
efeito estufa (GWP) de CH4 |
21 |
Mg CO2
suprem com gás equivalente / |
Schimel
et al., 1996 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
Mg
gás de CH4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
CO2
carbono equivalenteano |
-0,012 |
Milhões de Mg
CO2 - |
Calculado de
emissão de CH4, GWP, peso atômico de
C (12) e peso molecular de CO2 (44) |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
C/ano
equivalente |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
EMISSÃO ATRAVÉS DE TÉRMITAS DE FLORESTA |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Emissão/ha/ano
|
|
0,5 |
kg
CH4/ha/ano |
Fearnside,
1996b, |
|
|
|
|
|
|
||||||||||||||||||||||
|
Equivalentes
de Ha-ano de floresta |
0,6 |
Milhões de
equivalents de ha-ano |
Calculado a
partir de informações acima |
|
|
|
||||||||||||||||||||||||||
|
Emissão/ano |
|
317,0 |
Mg
CH4/ano |
Calculado a
partir de informações acima |
|
|
|
|
|
|
||||||||||||||||||||||
|
CO2
carbono equivalenteano |
0,0018 |
Milhões de Mg
CO2 - C/ano
equivalente |
Calculado como
acima |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
EMISSÕES DE INUNDAÇÃO NATURAL DE FLORESTA INUNDADA
PRE-REPRESA |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Emissão de
metano de floresta inundada durante inundação natural |
103,8 |
mg CH4/m2/dia.
Media de cinco estudos em floresta em várzea de água branca (Wassmann &
Martius, 1997, pág. 140) |
|
|
|
|||||||||||||||||||||||||||
|
Dias inundados
por ano |
59,4 |
Suposição de
dias, como acima. |
|
|
|
|||||||||||||||||||||||||||
|
Emissão anual
por km2 |
|
|
6,2 |
Mg CH4/ano/km2.
Calculatado a partir de informações acima |
|
|
|
|||||||||||||||||||||||||
|
Emissão natural
anual através de floresta inundada |
14.961 |
Mg CH4/ano.
Calculado a partir de informações acima |
|
|
|
|||||||||||||||||||||||||||
|
CO2
carbono equivalenteano |
0,086 |
Milhões de Mg
CO2 – Calculado a partir de informações acima |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
C/ano
equivalente |
|
|
|
|
|
|||||||||||||||||||||||
|
Emissão anual
anual ajustou para comprimento de ciclo |
|
|
44.883 |
Mg CH4/ano
Considering emissão por ciclo (2
vs de meses 6 meses) |
|
|
|
|
|
|||||||||||||||||||||||
|
CO2
carbono equivalenteano |
|
|
0,257 |
Milhões de Mg
CO2-equivalent Calculou de acima C/ano |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
EMISSÕES DE EVENTOS PERIÓDICOS DE FORMAÇÃO DE POÇAS
EM FLORESTA DE TERRA FIRME |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Formação de
poças em florestas de terra firme |
1,801 |
km2-dias/ano.
Calculado de área, 5% que inundam por evento (baseado em Mori & Becker,
1991) e presumiu freqüência de 5-ano e duração de 30 dias |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Emissão quando
inundado ou com formação de poças |
103,8 |
mg CH4/m2/dia.
Presumido ser o mesmo que a floresta de várzea (como acima). |
|
|||||||||||||||||||||||||||||
|
Emissão natural
anual através de formação de poças |
187,0 |
Mg CH4/ano.
Calculado a partir de informações acima |
|
|
|
|||||||||||||||||||||||||||
|
CO2
carbono equivalente/ano |
0,001 |
Milhões de Mg
CO2 - Calculado a partir de informações acima. C/ano equivalente |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
TOTAIS |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Emissão total
de metano |
43.259 |
Mg CH4/ano.
Calculado a partir de informações acima, incluindo ajuste de
comprimento do ciclo. |
|
|
|
|||||||||||||||||||||||||||
|
CO2
carbono equivalente/ano |
0,248 |
Milhões de Mg
CO2 - C/ano
equivalente. Calculado a partir de informações acima. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Tabela 7: Emissão evitada de óxido nitroso de perda
de floresta em Babaquara |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Item |
|
|
Valor |
Unidades |
Fonte |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
EMISSÕES DE FLORESTA NÃO
INUNDADA |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Emissão anual média de N2O do solo em
florestas não inundadas |
8,7 |
kg N2O/ha/ano |
Verchot et al.,
1999, pág. 37 |
|
|
|
|
|
|
|||||||||||||||
|
Área total de floresta inundada por reservatório |
6.004 |
km2 |
Baseado em 6.140 área de reservatório de km2
e leito fluvial de Revilla Cardenas, 1988, p.87, |
|
||||||||||||||||||||
|
Área de floresta inundada submersa pelo
reservatório |
2.427 |
km2 |
Revilla Cardenas, 1988, pág. 87 |
|
|
|||||||||||||||||||
|
Área de floresta de terra firme inundada por reservatório |
3.576 |
km2 |
Calculado por diferença |
|
|
|
|
|
|
|||||||||||||||
|
Fração do ano que floresta inundada é submersa
naturalmente |
0,17 |
Fração |
Assumido 2 meses média acesa |
|
|
|
|
|
||||||||||||||||
|
Emissão por ha por ano em floresta inundada |
7,23 |
kg N2O/ha/ano |
Proporcional ao tempo não inundado |
|
|
|||||||||||||||||||
|
Emissão por ano em floresta ribeirinha |
1.755,6 |
Mg N2O/ano |
Emissão por ha
X área de floresta inundada |
|
|
|||||||||||||||||||
|
Emissão por ano em floresta de firme de terra |
3.103,7 |
Mg N2O/ano |
Emissão por ha X área de floresta de terra firme |
|
|
|||||||||||||||||||
|
Emissão total por ano |
4.859,3 |
Mg N2O/ano |
Some através de tipo de floresta |
|
|
|
||||||||||||||||||
|
Potencial de efeito estufa (GWP) de N2O |
310 |
Mg CO2 suprem com gás equivalente / Mg gás de N2O |
Schimel et al., 1996 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
CO2 carbono
equivalenteano |
0,411 |
Milhões de Mg CO2 - C/ano equivalente |
Calculado de área e por-hectare emissão, peso
atômico de C (12) e peso molecular de CO2 (44) |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
EMISSÕES DE INUNDAÇÃO |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Inundação de floresta inundada |
404,6 |
km2-dias/ano |
Calculado de área e assumiu 6 meses de inundação em
médio |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Emissão de
formação de poças em florestas de terra firme |
1.801,1 |
km2-dias/ano |
Calculado de área, 5% que inundam por evento (baseado em Mori & Becker, 1991) e presumiu freqüência de 5 anos e uma duração de 30 dias |
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
Emissão quando inundada |
7,6 |
kg de N2O/km2-dia |
7.6 mg N2O/m2/dia( médias dos
reservatórios de Tucuruí e Samuel: de Lima et al., 2002) |
|
||||||||||||||||||||
|
Emissão de inundação de floresta inundada |
3,1 |
Mg N2O/ano |
Inundando (km2/dia) X emissão/km2/dia |
|
||||||||||||||||||||
|
Emissão de formação de poças em florestas de terra
firme |
13,7 |
Mg N2O/ano |
Formação de poças (km2-dias) X Emissão/km2/dia |
|
||||||||||||||||||||
|
Emissão total de inundação |
16,8 |
Mg N2O/ano |
Soma de emissões de inundação. |
|
|
|
|
|
||||||||||||||||
|
CO2 carbono equivalente/ano |
0,001 |
Milhões de Mg CO2 - |
Calculado de GWP como acima. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
C/ano equivalente |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
EMISSÃO TOTAL |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Emissão total de perda de floresta |
4.876,0 |
Mg N2O/ano |
Soma de floresta de não inundada, formação de poças
e emissões inundando |
|
|
|
||||||||||||||||||
|
CO2 carbono equivalenteano |
0.412 |
Milhões de Mg CO2 - |
Calculado de GWP como acima. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
C/ano equivalente |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Tabela 8: Aço usado na construção de Belo Monte e
Babaquara |
|
||||||||||
|
|
|
|
|
|
|
|
|||||
|
Belo Monte(a) |
|
|
|
|
|
||||||
|
|
Item |
Peso |
Número |
Massa total |
Totais por categoria |
|
|||||
|
|
|
(kN) |
|
(Mg) |
(Mg) |
|
|||||
|
Equipmento elétrico e mecânico |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
Turbinas-casa de força principal |
20.000 |
20 |
40.816 |
|
|
|||||
|
|
Condutos forçados |
14.150 |
20 |
28.878 |
|
|
|||||
|
|
Comportas da tomada d'água |
1.400 |
20 |
2.857 |
|
|
|||||
|
|
Peças fixas das comportas |
260 |
20 |
531 |
|
|
|||||
|
|
Comportas ensecadeiras da tomada d'água principal |
1.080 |
20 |
2.204 |
|
|
|||||
|
|
Peças fixas das comportas ensecadeiras |
157 |
20 |
320 |
|
|
|||||
|
|
Portico rolante da tomada d'água |
1.700 |
1 |
173 |
|
|
|||||
|
|
Grades da tomada d'água |
410 |
8 |
335 |
|
|
|||||
|
|
Viga pescador das grades |
60 |
1 |
6 |
|
|
|||||
|
|
Máquinas limpa grades |
260 |
2 |
53 |
|
|
|||||
|
|
Comportas ensecadeiras dos tubos de sucção |
940 |
2 |
192 |
|
|
|||||
|
|
Peças fixas-comportas ensecadeiras |
110 |
2 |
22 |
|
|
|||||
|
|
Portico dos tubos de sucção |
550 |
1 |
56 |
|
|
|||||
|
|
Pontes rolantes da casa de força |
4.800 |
2 |
980 |
|
|
|||||
|
|
Ponte rolante auxiliar (Galeria do SF6) |
180 |
1 |
18 |
|
|
|||||
|
|
Comportas-vertedouro principal |
2.300 |
17 |
3.990 |
|
|
|||||
|
|
Peças fixas - comportas do vertedouro principal |
52 |
17 |
90 |
|
|
|||||
|
|
Comportas-ensecadeiras de montante |
2.380 |
2 |
486 |
|
|
|||||
|
|
Peças fixas-comportas ensecadeiras de montante |
159 |
7 |
114 |
|
|
|||||
|
|
Comportas ensecadeiras de jusante |
1.228 |
2 |
251 |
|
|
|||||
|
|
Peças fixas de comportas ensecadeiras de jusante |
191 |
2 |
39 |
|
|
|||||
|
|
Portico rolante de montante (& Tomada d'água
complementar) |
520 |
1 |
53 |
|
|
|||||
|
|
Portico rolante de jusante (& casa de força
complementar) |
800 |
1 |
82 |
|
|
|||||
|
|
Turbinas-casa de força complementar |
3.000 |
7 |
2.143 |
|
|
|||||
|
|
Comportas emergência (jusante) |
715 |
7 |
511 |
|
|
|||||
|
|
Comportas ensecadeiras tomada d'água complementar |
952 |
4 |
389 |
|
|
|||||
|
|
Peças fixas-comportas ensecadeiras tomada d'água
complementar |
78 |
4 |
32 |
|
|
|||||
|
|
Portico rolante -tomada d'água complementar |
520 |
1 |
53 |
|
|
|||||
|
|
Grades da tomada d'água complementar |
305 |
4 |
124 |
|
|
|||||
|
|
Peças fixas-grades da tomada d'água complementar |
68 |
4 |
28 |
|
|
|||||
|
|
Máquinas limpa grades-tomada dágua complementar |
260 |
1 |
27 |
|
|
|||||
|
|
Comportas ensecadeiras dos tubos de
sucção-complementar |
603 |
2 |
123 |
|
|
|||||
|
|
Peças fixas-comportas ensecadeiras dos tubos de
sucção-complementar |
42 |
2 |
9 |
|
|
|||||
|
|
Portico rolante dos tubos de sucção-complementar |
800 |
1 |
82 |
|
|
|||||
|
|
Pontes rolantes da casa de força complementar |
440 |
2 |
90 |
|
|
|||||
|
|
Comportas do vertedouro complementar |
3,050 |
4 |
1,245 |
|
|
|||||
|
|
Peças fixas - comportas do vertedouro complementar |
61 |
4 |
25 |
|
|
|||||
|
|
Comportas ensecadeiras de montante - complementar |
2,976 |
1 |
304 |
|
|
|||||
|
|
Peças fixas - comportas ensecadeiras de montante -
complementar |
242 |
1 |
25 |
|
|
|||||
|
|
Portico rolante -vertedouro complementar |
580 |
1 |
59 |
|
|
|||||
|
|
Peças fixas-portico rolante vertedouro complementar |
120 |
1 |
12 |
|
|
|||||
|
|
Geradores-casa de força principal |
27,200 |
20 |
55,510 |
|
|
|||||
|
|
Geradores-casa de força complementar |
1,770 |
7 |
1,264 |
|
|
|||||
|
|
Sub-total |
|
|
|
144,598 |
|
|||||
|
|
|
|
|
|
|
|
|||||
|
Concrete reinforcing bars |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
Armadura de concreto - casa de força |
|
|
80,715 |
|
|
|||||
|
|
Armadura de concreto - túnel de desvio |
|
|
850 |
|
|
|||||
|
|
Armadura de concreto - transições e muros de
concreto |
|
|
7,348 |
|
|
|||||
|
|
Armadura de concreto -Vertedouros de superfície |
|
|
9,836 |
|
|
|||||
|
|
Armadura de concreto -Tomada d'água e adutoras |
|
|
63,442 |
|
|
|||||
|
|
Armadura de concreto -Canal de adução |
|
|
16,472 |
|
|
|||||
|
|
Armadura de concreto -Canal e/ou túnel de fuga |
|
|
72 |
|
|
|||||
|
|
Sub-total |
|
|
|
178,735 |
|
|||||
|
Total steel at Belo Monte |
|
|
|
323,333 |
|
||||||
|
|
|
|
|
|
|
|
|||||
|
Babaquara |
|
|
|
|
|
||||||
|
|
Calculation of concrete volume as proportional to Belo Monte |
|
|
|
|||||||
|
Electrical and mechanical
equipment(b) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
Installed capacity at Belo
Monte |
11,181.3 |
MW |
|
|
|
|||||
|
|
Installed capacity at
Babaquara |
6,274 |
MW |
|
|
|
|||||
|
|
Electro-Mechanical steel at
Belo Monte |
144,598 |
Mg |
|
|
|
|||||
|
|
Proportional electrical and
mechanical steel at Babaquara |
81,136 |
Mg |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
Concrete reinforcing bars |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
Concrete volume at Belo
Monte |
4,355,480 |
m3 |
|
|
|
|||||
|
|
Concrete volume at
Babaquara |
5,410,000 |
m3 |
|
|
|
|||||
|
|
Concrete reinforcing bars
at Belo Monte |
178,735 |
Mg |
|
|
|
|||||
|
|
Proportional weight of reinforcing
bars at Babaquara |
222,009 |
Mg |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
Total steel at Babaquara |
303,146 |
Mg |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
(a) Data source: Brazil, ELETRONORTE, 2002. |
|
||||||||||
|
(b) In addition to the listed items, the
following lack information on their weight in the viability study:
subestações elevadoras: principal (1), complementar (1), transformadores
elevadores: principal (22), complementar (5) |
|
||||||||||
|
(c) Babaquara concrete from da Cruz, 1996, p. 18. |
|
|
|||||||||
|
Tabela 9:
Cimento usado para construção de Belo Monte e Babaquara |
||||||||
|
|
|
|
|
|
|
|||
|
Belo Monte |
|
|
|
|
||||
|
|
|
Cimento |
|
Nota |
|
|||
|
|
|
(Mg)(a) |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
Casa da força |
215.664 |
|
|
|
|||
|
|
Túnel de desvio |
1.780 |
|
|
|
|||
|
|
Transições e
muros de concreto |
42.882 |
|
|
|
|||
|
|
Vertedouros de
superfície |
48.049 |
|
|
|
|||
|
|
Tomada d'água e
adutoras |
183.951 |
|
|
|
|||
|
|
Canal de adução |
356.160 |
|
|
|
|||
|
|
Canal e/ou
túnel de fuga |
180 |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
Total |
848.666 |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
Babaquara |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
Cálculo de
cimento de volume concreto |
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
Volume concreto
em Babaquara |
5.410.000 |
m3 |
(b) |
|
|||
|
|
Conteúdo de
cimento médio de concreto |
225 |
kg/m3
|
(c)
|
|
|||
|
|
Uso de cimento
calculado a Babaquara |
1.217.250 |
Mg |
|
|
|||
|
|
|
|
|
|
|
|||
|
(a) Fonte de
dados: Brasil, ELETRONORTE, 2002. |
|
|
|
|||||
|
(b) da Cruz,
1996, pág. 18 |
|
|
|
|
||||
|
(c) Conteúdo
médio de cimento de 52 barragens suiças: 225 kg/m3 (Dones &
Gantner, 1996) |
|
|||||||
|
|
|
|
|
|
|
|||
|
Tabela 10:
Emissões de gás de efeito estufa de represa e construção de transmissão-linha
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Belo Monte |
|
|
|
Babaquara |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Item |
|
Unidades |
Emissão por unidade CO2-
equivelente C
(kg) |
Ref - erencia |
Nota |
No. of unidades |
Ref - erence |
Emissão (milhões Mg CO2
- equivalente C) |
Nota |
No. of unidades |
Ref - erencia |
Emissão (milhões Mg CO2
- equivalente C) |
|
||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Aço |
|
Mg
|
600,0 |
(a)
|
(b) |
323.333 |
(c) |
0,194 |
(a) |
303.146 |
(c)
|
0,182 |
|
||
|
Cimento
|
|
kg
|
0,207 |
(a) |
(c) |
848.666.000 |
(e) |
0,176 |
(a) |
1.217.250.000 |
(e) |
0,252 |
|
||
|
Diesel |
|
milhões de kg |
863.280 |
(d)
|
|
135,1 |
(f)
|
0,117 |
|
76,8 |
(f)
|
0,066 |
|
||
|
Eletricidade
|
|
TWh |
139.903.200 |
(g) |
|
3,15 |
(h) |
0,441 |
|
1,79 |
(h) |
0,251 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Substituto-total
de represa |
|
|
|
|
|
|
0,928 |
|
|
|
0,751 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Construção de
linha de transmissão |
km-MW instalado
|
1,9 |
(i)
|
|
29.596.901 |
(j)
|
0,055 |
(a)
|
17.046.458 |
(j)
|
0,032 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Total de
projeto |
|
|
|
|
|
|
0,983 |
|
|
|
0,783 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(a) Van Vate,
1995. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(b) Usa GWPs de
100 anos de IPCC 1994: CO2=1, CH4=24.5, N2O=320
(Albritton et al., 1995). |
|
||||||||||||||
|
(c) Tabela 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(d) Usa GWPs de
100 anos de IPCC 1995 [Kyoto Protocol
valores]: CO2=1, CH4=21, N2O=310 (Schimel et al., 1996). |
|
||||||||||||||
|
(e)) Tabela 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(f) Uso de
diesel en Babaquara considerado proporcional à escavação planejada. |
|
||||||||||||||
|
(g) Baseado em
subsituição de gás de ciclo combinado em São Paulo (veja texto). |
|
|
|
||||||||||||
|
(h) Uso de
eletricidade na construção baseado em 280 kWh de electricidade por TJ (Dones
& Gantner, 1996). Emissões de eletricidade consideram o baseline de
geração de gás natural no São Paulo (veja texto). |
|
||||||||||||||
|
|
|||||||||||||||
|
(i) Média em
Québec, Canadá (Peisajovich et al.,
1996). |
|
|
|
||||||||||||
|
(j) A linha de
transmissão de Belo Monte até a rede do centro-sul brasileiro vai para três
destinos com uma distância má de 2647 km: Cachoeira
Paulista-SP (2.662 km), Campinas-SP (2.599 km) e Ouro Preto-MG (2.680 km)
(Brasil, MME-CCPESE, 2002). Babaquara
tem 70 km adicionais de linha. |
|
||||||||||||||
|
Tabela 11: Médias a longo prazo de emissão líquida
de gases de efeito estufa para o complexo Belo Monte/Babaquara |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Emissões de
todas as fontes (milhões de Mg
C CO2-equivalente /ano) |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Anos 1-10 média de 10 anos |
Anos 1-20 média de 20 anos |
Anos 1-50 média de 50 anos |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
Emissões de
inventário |
|
|
|
|
|
|
|
|
|
|
Emissões de
superfície |
|
|
1,0 |
0,8 |
0,4 |
|
|
|
|
Turbinas
|
|
|
|
2,6 |
3,8 |
2,8 |
|
|
|
Vertedouro
|
|
|
|
1,6 |
1,0 |
0,6 |
|
|
|
Canal
de adução |
|
|
0,2 |
0,4 |
0,3 |
|
|
|
|
Gargalos |
|
|
0,01 |
0,01 |
0,01 |
|
|
|
|
Emissões de
inventário totais |
|
5,3 |
6,0 |
4,1 |
|
||
|
Outros fluxos |
|
|
|
|
|
|
|
|
|
|
Substituição de
fóssil-combustível |
|
-3,7 |
-3,9 |
-4,1 |
|
||
|
|
Fluxos de
ecossistema pre-represa |
|
-0,3 |
-0,5 |
-0,6 |
|
||
|
|
Biomassa acima
d’água |
|
|
9,6 |
7,2 |
3,8 |
|
|
|
|
Decomposição no
perímetro da magem |
|
|
0,07 |
0,04 |
0,01 |
|
|
|
|
Outros fluxos
totais |
|
|
5,9 |
0,1 |
-5,5 |
|
|
|
Impacto
total |
|
|
|
11,2 |
6,1 |
-1,4 |
|
|
|
Impacto total
como múltiplo da emissão de referência de combustível fóssil |
|
|
4,0 |
2,5 |
0,7 |
|
||















