The text that follows is a PREPRINT.

Please cite as:

Nogueira, E.M., B.W. Nelson and P.M. Fearnside. 2006. Volume and biomass of trees in central Amazonia: Influence of irregularly shaped and hollow trunks. Forest Ecology and Management 227(1-2): 14-21.

DOI 10.1016/j foreco 2006.02.004

ISSN: 0378-1127

The original publication is available at: http://www.elsevier.com.nl <publisher link>

Ms. No. FORECO1257

Volume and biomass of trees in central Amazonia: Influence of irregularly shaped and hollow trunks

Euler Melo Nogueira^a; Bruce Walker Nelson^b, Philip M. Fearnside^b*

^aProgram in Tropical Forest Science, National Institute for Research in the Amazon–INPA, C.P. 478, 69.011-970 Manaus, Amazonas, Brazil.

^bDepartment of Ecology, National Institute for Research in the Amazon–INPA, C.P. 478, 69.011-970 Manaus, Amazonas, Brazil.

* Corresponding author. e-mail: pmfearn@inpa.gov.br

Revised 5 Feb. 2006

Main text 4612 words; total 5989 words.

Abstract

Conventional measurements of diameter, basal area and volume of the bole assume that any cross section of the bole is circular and that the bole is a solid of revolution. These assumptions lead to error when the bole is irregularly shaped and/or hollow. These errors were quantified for trees in central Amazonia after adjusting the number of trees sampled in each class based on the diameter distribution of a large inventory. For large trees (DBH ≥ 50 cm) total basal area was overestimated by 30%, while the overestimate was 11% for all trees with DBH ≥ 5 cm. The total bole volume per hectare was overestimated by 11.2% (~40 m³/ha). Most of this volume correction is attributed to the non-circular form of the cross section; the effect of hollow areas on the volume of the bole was only 0.7%. For trees above 31.8 cm DBH, which is the minimum diameter in the Projeto RADAMBRASIL inventories, the volume per hectare was overestimated by 4.4% using conventional measurements. Because of compensating errors in commonly used formulas, however, the volume overestimate associated with conventional methods does not imply biomass overestimation in studies that have used the RADAMBRASIL dataset.

Keywords: irregularities of the bole, volume of the bole, hollow trees, basal area, biomass.

1. Introduction

Estimates of emissions of greenhouse gases from deforestation and logging in Brazilian Amazonia are derived from estimates of biomass obtained from large-scale inventories of wood volume. Occurrence of irregular and hollow boles can directly affect the estimates of volume and of greenhouse gas emissions from the region. This is because measures of diameter, basal area and wood volume invariably treat the bole as a solid of revolution, making the assumption that any cross section of the bole is circular (Ahrens and Holbert, 1981). In tropical forests, trees with indentations and irregularly shaped boles lead to overestimates in the measures of basal area and volume when using a measuring tape, even when diameter is measured above any buttresses or protuberances (Clark, 2002; Clark and Clark, 2000; Sheil, 1995). The errors are larger in species that have accentuated irregularities in the bole, such as Aspidosperma discolor A.DC. (Carapanaúba) and Minquartia guianensis Aubl. (Acariquara), and in large trees, which tend to have more irregularities and higher frequencies of hollow trunks (Clark and Clark, 2000; Fearnside, 1992, 1997a).

The occurrence of hollow trunks can also mean significant overestimates in measurements of basal area and of real wood volume, this being one of the uncertainties in estimates of biomass and of carbon emissions based on forest inventories (Brown and Lugo, 1992; Fearnside, 2000). Hollow trees are important in forest-management plans and are associated with the presence of termites (Amelung et al., 2002) and treefalls caused by wind and lianas (Putz et al., 1983); these affect turnover rate, average stand age, and rates of gap formation and consequent recruitment of pioneers. For Amazonia, estimates of hollow volume have varied from 1.6% to 9.2% of the total volume of the boles per unit of area (Fearnside, 1992, 1997b, 2000; Brown et al., 1995; Brown and Lugo, 1992).

Irregular and hollow boles will not influence biomass estimates that are based on direct weighing of trees or on allometric equations derived from directly weighed trees, but these characteristics of the boles will affect biomass estimates derived from commonly used wood volume data. In this paper we evaluate the effect of irregularities in the bole and the occurrence of hollow trunks on the measurements diameter and basal area for trees in Amazonia. These findings have important implications for estimates of forest volume and biomass and for carbon emissions from deforestation.

2. Materials and Methods

2.1. Collection site

The collection areas were six sites spread over ~45 km² in the Tarumã Small-Farmer Rural Settlement Project, centered about 50 km northwest of Manaus, Amazonas, Brazil (60.16ºW; 2.83ºS). Average annual precipitation is 2075 mm, with July to September being <100 mm/month; mean altitude is 100 m; mean monthly temperature ranges from 26 ºC to 27.6 ºC (INMET, 2003). The vegetation is dense upland rain forest without seasonal flooding, on nutrient-poor yellow latosol (Oxisol)(Magnago et al., 1978; Yamazaki et al., 1978). The six sites chosen were in primary forest, without recent natural gaps or growth of pioneers associated with deforestation borders. The area is a new colonization front (< 5 years old) and deforestation for agriculture was authorized by the Brazilian Institute for the Environment and Renewable Natural Resources (IBAMA). A total of 303 trees (DBH ≥ 5 cm) were felled in the field at random, but following pre-defined quotas by size class. An inventory of 72 ha (Castilho, 2004) was then used to adjust the felled sample using a distribution of tree diameters normally found in forests (diameter classes 5-cm DBH intervals). The numbers used to adjust the frequency of sampled trees to match that found in the forest are based on the 72 ha inventoried by Castilho (2004) and are termed “replication factors” in this paper (Table 1).

[Table 1 here]

2.2. Evaluation of circumference measures for obtaining the volume of the bole.

For the 303 trees botanical samples were collected and disks of constant thickness (~3 cm) were removed with a chainsaw. Disks were taken at breast height and at the top of the bole, below the thickening associated with the base of the first major branch. For 73 trees chosen randomly from the full sample of 303 trees, two additional disks were taken, positioned at 33% and 66% of the length between breast height and the height of the first major branch. For all trees measurements were made of total height, height of the bole and circumference as determined with a measuring tape at each disk-sampling point. The measurements at breast height were made 1.36 m above the ground or above the buttresses, if present. Each disk’s outline was drawn on a large sheet of paper by tracing the outer edge and inner hollows if present. The drawings were affixed to a flat wall and photographed with an 80-mm lens from a standard distance of 4 m using a digital camera. The average pixel size in the digital photographs was 1.876 mm on each side, determined using four reference marks on the wall. The view angle was perpendicular and scale varied by only 0.6% from the center to the edge of the panel.

Using Adobe Photoshop 4.0 software (Adobe Systems, Inc., 1996) all of the pixels were selected that corresponded to areas with wood, using the image with amplification of 600%. The area was determined in pixels, converted to square centimeters and compared with the cross-sectional area obtained by the conventional method, which considers the perimeter taken with a measuring tape in the field to be the circumference of a perfect circle and without any hollows. Three corrected biometric attributes for each tree (diameter, basal area and volume) were calculated from the true area of sections of the bole, as determined by the pixel count, thereby correcting for the effects of non-circular shape and hollow trunks. The corrected diameter would be, for example, the diameter calculated for a perfect circle with an area equal to that determined by the pixel count of the section cut from a tree. Oval sections, irregularities and the presence of hollow areas mean that the “conventional” biometric attributes will be larger than the “corrected” attributes (Figure 1 and Table 2).

From the corrected cross–sectional areas, the volume of each bole was calculated using the Smalian formula: {(Asi + Asf) / 2} × h; where Asi = area of the cross section at breast height, Asf = height at the top of the bole; and h = height of the commercial bole. This procedure was adopted for the 73 trees for which cross sections were sampled at four positions along the bole, and also for the other 230 trees for which cross sections were only sampled at breast height and near the first large branch.

2.3. Botanical identification

Herbarium vouchers from each tree were identified by practical botanical experts (parabotanists) who were employees of the herbarium of the National Institute of Research in the Amazon (INPA). For the 303 trees sampled randomly, 186 different species or morpho-species were identified. Voucher specimens are kept at INPA.

3. Results

3.1. Effect of non-circular form and of hollows on conventional estimates of diameter, basal area and wood volume

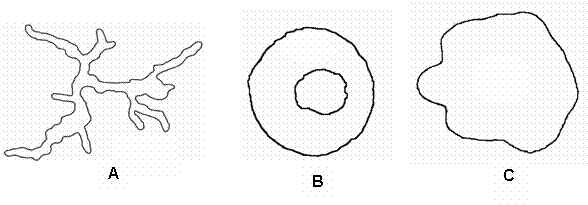
For species with irregularities in the bole, the conventional measurements of basal area can overestimate by up to 400% the real cross-sectional area of wood with bark at breast height (Figure 1 and Table 2). When the sample of 303 trees was adjusted to represent the true frequency distribution of diameter classes in terra firme (upland) forest in central Amazonia, the corrected diameter was, on average, 3.7% smaller at breast height and 3.1% smaller at the top of the bole, when compared with the diameter obtained in the conventional way (from determining the girth with a measuring tape and assuming this value to be the circumference of a circle).

[Figure 1 and Table 2 here]

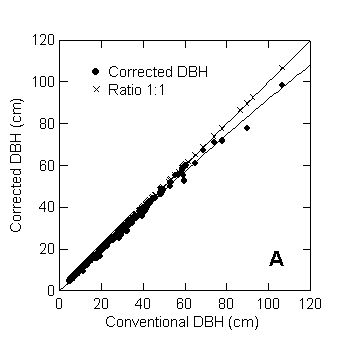
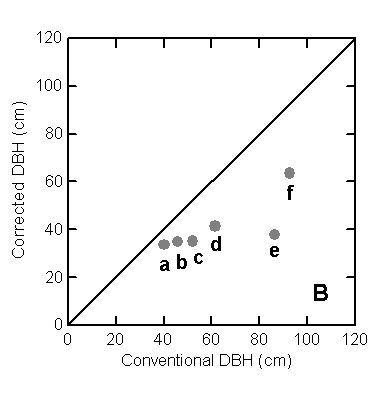
The overestimate in the diameter measures caused by the non-circular shape and hollow trunks is greater for large trees (Figure 2a). For trees with DBH ≥ 50 cm, adjusted to their frequency in a large inventory (i.e., “inventory-adjusted” by use of the replication factors; see Table 1), the mean conventional DBH was 14.5% larger than the mean corrected DBH; about half of this effect was caused by six trees with very irregular boles, most of which are illustrated in Figure 2b. These six trees had conventional DBH that varied from 45 to 92 cm. At the top of the bole, the average overestimate of the diameter was 8.6% for the same size class (DBH ≥ 50 cm). The cross section becomes more circular in higher parts of the bole.

[Figure 2 here]

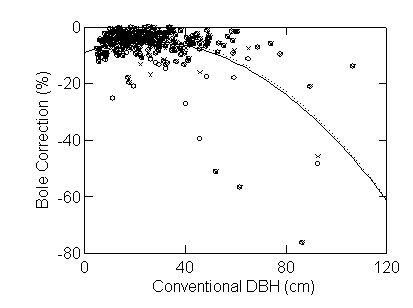
By the conventional method, the inventory-adjusted basal area/ha was 11% larger than the corrected basal area. The six trees with very irregular boles were responsible for about one-third of this effect. Inventory-adjusted mean overestimate of the area of the disk per tree was 6.6% at breast height and 6% at the top of the bole (Figure 3). The error is again greater for large trees. For trees with DBH ≥ 50 cm, the overestimate of the cross-sectional area at breast height averaged 30%, about half of this (14%) being caused by the six trees with very irregular boles. The median overestimate of basal area was only 12% for all trees >50 cm DBH.

[Figure 3 here]

Considering all trees with DBH ≥ 5 cm, conventional measurements resulted in a mean overestimate per inventory-adjusted tree of 6.5% in the volume of the bole and of 11.2% in the bole volume per hectare. This is an overestimate of about 40 m³/ha. Again, about one-third of this (4%) was due to the six large trees with highly irregular cross sections. For trees with DBH ≥ 50 cm (n = 23) the inventory-adjusted overestimate of stand bole volume was of 24%, half of this being due to the six highly irregular trees. The 23 large trees were also responsible for almost half of the error per hectare, or approximately 24 m³/ha. 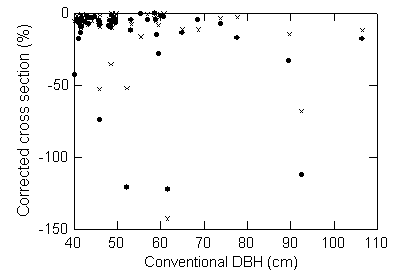The difference in the estimate of volume was again greater for larger trees (Figure 4). The trees with the largest overestimates of volume using conventional measures of diameter were: Minquartia guianensis Aubl. (common name Acariquara, DBH = 45.8 cm), 65.6% overestimated volume; Chimarrhis turbinata DC. (Madeira-do-Remo, DBH = 92.5 cm), 94%; Aspidosperma discolor A.DC. (Carapanaúba, DBH = 52.2 cm), 105.1%; Aspidosperma discolor A.DC (Carapanaúba, DBH = 61.6 cm), 130.6%; and Swartzia polyphylla DC. (Paracutaca, DBH = 86.4 cm), 320.7%.

[Figure 4 here]

The volumetric estimate obtained with conventional DBH and the formula (eq. 1) used by Projeto RADAMBRASIL (1978-1983; sheet 20A, volume 18, p. 17), when compared with the “corrected” (Smalian) volume, was 6.3% larger (inventory-adjusted mean per tree), considering only those trees above the minimum diameter inventoried by RADAMBRASIL (31.8 cm DBH). For volume per hectare of trees with DBH ≥ 31.8 cm, the overestimate was only 4.4% (n = 93 prior to replication). This is much smaller than the 15.3% overestimate found for bole volume per hectare for trees with DBH ≥ 31.8 cm calculated by the Smalian method and conventional DBH .

V = π/4 × DBH² × H × FF (eq. 1)

Where:

V = Volume with bark (m³)

DBH = Diameter at breast height (m)

H = Commercial height (m)

FF = Form factor: 0.7.

3.2. Occurrence of hollow trees

Hollow areas of different sizes were found in only 30 of the 303 trees sampled (Table 3). The lowest disk (taken at 1.36 m or above any buttresses) was the most frequent location for hollows. But at this height, only 7.7% of the sampled trees had hollows and these, when present, occupied an average of only 9% of the cross-sectional area. In just 3.2% of the sampled trees, hollow areas were found at the top of the bole. Only one of the 303 trees had hollow area at both the top of the bole and at breast height, possibly being hollow along the entire length of the bole.

The sum of the individual basal areas of all trees indicates that the hollow areas at breast height or just above the buttresses occupied only 1.1% of the total cross-sectional area of the sample. At the top of the bole, the hollow area represented 0.8% of the total area at this height for all trees. Hollows larger than 30% of the cross-sectional area of the bole were not found at any height. With respect to the total area of the cross section of the bole, 24 of the 303 trees had hollow areas that occupied up to 10% of the cross-sectional area; in 8 trees hollows occupied 10 to 20%, and in 5 trees the hollow area occupied 20 to 30%.

[Table 3 here]

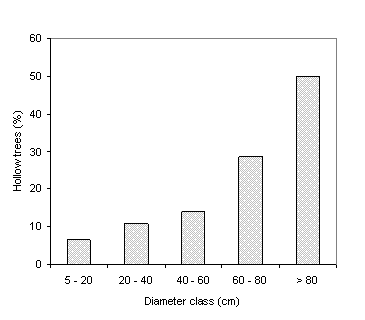
For the sampled trees, hollow trunks were more frequent in trees with larger diameters (Figure 5). When the occurrence of hollow areas was ignored, volume was overestimated by only 0.6% in the 303 sampled trees and the bole volume per hectare was overestimated by 0.7% for all trees, as compared to the volume obtained from DBH corrected for the effects of irregularites and hollows (Smalian formula). This is because hollow areas occur mainly in large trees, and these did not need to be replicated when adjusting to inventory frequencies.

[Figure 5 here]

4. Discussion

4.1. Effect of non-circular cross section and of hollow trunks on measures of diameter, basal area and wood volume

The effects of irregularities of the bole and of buttresses on estimates of diameter, basal area, volume and biomass have been evaluated in tropical forests (Clark, 2002; Clark and Clark, 2000; Sheil, 1995), but there are no studies that separate the effects buttresses and of non-circular shapes (including those above any buttresses). Discussion in the literature has focused on the effects of buttresses and hollows as sources of bias in measures of biometric attributes, with possible effects on biomass estimates. Indeed, diameter measures at breast height in trees with buttresses have been the source of intense debate on the apparent temporal trend of increasing biomass in permanent plots of Neotropical forests (Clark, 2002; Clark and Clark, 2000), increasing the list of uncertainties concerning the role of tropical forests as a source or a sink of carbon (Houghton, 2003). The occurrence of hollow trunks has also been considered as a bias towards overestimation in biomass calculations, up to 9% being discounted in recent estimates of carbon emissions (Fearnside, 2000).

The results of the present study point to new considerations: (i) the irregular form of the boles of the large trees and species with accentuated indentations can lead to overestimation of biometric attributes, (ii) the occurrence of hollow trunks seems to cause little error in the estimates of wood volume. For the first effect, and at the stand level, the importance of irregularities in the bole will be highly sensitive to the stand density of species with very irregular boles and to the greater effect of irregularities in large trees. Forests with high density of species with irregular boles can contain an important bias towards overestimation. The errors caused by irregularities and hollow trunks are more important for forest biomass than the average bias per tree would suggest because the biases are more accentuated in the large trees that represent a substantial amount of wood volume per hectare. In spite of the forests of central Amazonia having less biomass in large trees, as compared to other areas in Amazonia (see Chave et al., 2001), the percentage reaches 23% in trees with DBH ≥ 50 cm according to an estimate of biomass in 20 ha in central Amazonia (do Nascimento, 2002).

On the other hand, the difference between conventional and corrected stand volume cannot be applied in a simple fashion to correct stand biomass estimates downward. This is because allometric regressions relate conventional DBH to true stand biomass in felled and weighed samples. Therefore, the independent variable that must be used in biomass estimates is the conventional (not the corrected) DBH. Biomass errors in a forest inventory can be in either direction, depending on how the importance of irregularities and hollows in that inventory compares with the (unfortunately unknown) importance of these factors in the felled and weighed trees used to derive allometry.

Commercial volume is based on large trees and will be overestimated using geometric formulas (such as equation 1). The correction factor is both greater and more uncertain for large trees (Figures 2a, b). The error can be minimized if the volumes of species with very irregular boles are estimated separately. Large-scale inventories carried out in Amazonia, such as Projeto RADAMBRASIL, included species with highly irregular boles in their volume estimates. The Smalian formula, based on the conventional measurements of diameter or circumference, has been applied to obtain volumes used as reference values in developing and validating models (Ribeiro, 1996, p. 23; Moura, 1994, p. 29; Higuchi and Ramm, 1985, p. 35; Fernandes et al., 1983, p. 539). Naturally, the errors will be smaller in the models in which the dependent variable was obtained using only species with boles that were more regular and free of defects, as assumed by Fernandes et al. (1983). Such models are appropriate for commercial wood species, but not for estimating the total volume per unit area in a community. Species with very irregular boles also generate significant amounts of waste when logged, and volumetric models developed for commercial logging always result in overestimates for these species.

4.2. Hollow trees

Hollows were more frequent and were larger toward the base of the bole. In only one of the 303 trees was a hollow area found at both ends of the bole. In the 73 trees sampled at four positions, no hollows were found in the slice 2/3 of the way up the bole. However, the number of observations was too small to make inferences about the continuity of hollows in every bole, since hollows were found in only 10% of the trees. Considering all trees that were hollow at breast height, among the 303 trees in the study, the total hollow area would be equivalent to a single bole of just 25 cm diameter. The effect of hollows on bole volume was determined by transforming trees into thinner volumes of revolution using the true cross-sectional area of wood at the position of each disk, then applying the Smalian formula. The effect of hollows on the total bole volume per hectare was small: a reduction of only 0.7%. This observation will increase the estimates of carbon emission from deforestation in Amazonia, such as those of Fearnside (1992, 1997b, 2000), which used Projeto RADAMBRASIL data and discounted by 6.6-9.2% for hollow boles. However, the percentage found here is close to that reported by Brown and Lugo (1992). For RADAMBRASIL data, these authors assumed, that hollows occupy 2% of the total bole volume/ha, giving a 1.6% downward correction for stand biomass estimates by assuming that 20% of the boles with DBH ≥ 40 cm are hollow up to 2 m above the ground. A similar percentage was found by Clark and Clark (2000) in tropical forest plots in Costa Rica, where the hollow area was estimated at 1.7% of the total volume of boles with diameter above 30 cm. For open forests in Rondônia, Brown et al. (1995) found hollow areas in less than 20% of 53 boles examined and estimated that the total hollow volume at less than 4%. These numbers indicate that the occurrence of hollow areas can, in fact, represent little bias in the biomass estimates. However, it should be pointed out that in the study in question the estimate of 0.7% hollow volume (only in the volume of the bole) is indirect because the height of each hollow area was not appraised along the length of the bole. For trees with DBH over 40 cm, the percentage of hollow areas found in this study (13%) was much smaller than the 27% reported for central Amazonia by Fearnside (1997b), based on N. Higuchi (personal communication). For trees over 10 cm DBH (n = 145), an even higher percentage (32%) was reported by Rodrigues and Valle (1964) for trees of sandy soil forests in central Amazonia.

4.3. Effect of non-circular and hollow trunks on the biomass estimates

The results reported here do not affect biomass estimates that are based on direct weighing of trees or on allometric equations derived from weighed trees. However, estimates of wood volume in inventories could be overestimated but have this bias offset by other variables used in the formula that is adopted for the biomass estimate. A more detailed explanation can clarify this result.

The biomass estimates carried out starting from volumetric data are based on forest inventories that are the only available sources of data with broad spatial representativeness (Brown and Lugo, 1992; Brown et al., 1989, 1991), according to the model:

TAGB = Inventoried volume × VEF × WD × BEF (eq. 2a)

Where:

TAGB = Total above-ground biomass of standing trees ≥ 10 cm DBH (Mg ha^-1),

Inventoried volume = Commercial volume of the boles above inventoried minimum DBH (m³ ha^-1),

VEF = Volume expansion factor, representing the volume of boles of trees with DBH between 10 cm and the minimum inventoried DBH,

WD = Wood density (g cm^-3);

BEF = Biomass expansion factor (adds the biomass of the crown, for all trees ≥ 10 cm DBH).

The above model has been used to obtain biomass estimates per hectare for Brazilian Amazonia starting from RADAMBRASIL inventories that, as demonstrated, report overestimated values of wood volume due to irregularities and hollow trunks. However, it is necessary to evaluate how the effects of irregularities and hollow trunks reported in the present study will influence estimates of biomass and of carbon emissions.

The variables in equation 2a assume the following values, according to Houghton et al. (2001), Brown (1997), Brown & Lugo (1992) and Brown et al. (1989):

VEF = 1.25 for dense forests and 1.5 for other Amazonian forests;

WD = 0.69 g cm^-3;

BEF = exp{3.213 - 0.506 Ln SB}, for SB < 190 Mg ha^-1;

BEF = 1.74, for SB > 190 Mg ha^-1;

SB = Stand biomass (biomass of boles ≥ 10 cm DBH) = Inventoried volume × VEF × WD

Brown (1997, p. 6) presents another equation (eq. 2b), which is included here for comparison with the approach of Houghton et al. (2001):

TAGB = VOB × WD × BEF (eq. 2b)

Where:

TAGB = Total above-ground biomass of standing trees ≥ 10 cm DBH (Mg ha^-1)

WD = Wood density;

BEF = Biomass expansion factor (adds crown biomass, for all trees ≥ 10 cm DBH),

VOB = Volume over bark of the boles of all trees ≥ 10 cm DBH (m³ ha^-1).

Estimates of "total above-ground biomass (TAGB)" based on Brown and Lugo (1992), in the equations above (2a, b), only refer to the live-tree component ≥10 cm DBH. For estimates of TAGB, it has been suggested that the equation may result in bias due to the occurrence of hollow trunks (Fearnside and Laurance, 2003) when using the model of Brown and Lugo (1992), or Houghton et al. (2001). However, in a recent publication, Fearnside and Laurance (2004) eliminate the corrections originating from hollow areas, and conclude that the volume estimates based on Brown et al. (1989) do not need corrections for this factor. Corrections for irregularities in the bole are not needed when adopting the model of Brown and Lugo (1992). First, it is necessary to review the development of three models:

BEF = exp{3.213 - 0.506 Ln SB}, for SB < 190 Mg ha^-1 (eq. 3)

BEF = 1.74, for SB > 190 Mg ha^-1; (eq. 4)

BEF = TAGB × (SB)^-1 (eq. 5)

The model in equation 5 was the basis for obtaining the coefficients presented in equation 3 and the constant value of BEF in equation 4. It was based, in 1989, on the “known” values of TAGB and SB for 32 plots in humid forest, almost all in Venezuela (Brown et al., 1989). The known values of TAGB were actually indirect estimates derived using allometric models for individual trees, starting from D, H and WD (diameter at breast height, total height and wood density, respectively), according to equation 6:

Dry biomass = 0.0899 (D² × H × S)^0.9522 (eq. 6)

The values of SB were also estimated using D (measured in the field), commercial H (measured in the field), form factor of 0.7, and WD, this last being obtained from tables for 65% to 85% of the species in the 32 inventories, or, in the case of the species with unknown WD, from the average of WD of the known species.

Because many estimates of Amazonian biomass are ultimately derived from the Venezuelan data (e.g., equation 6), the interpretation of any errors in the estimate of SB (biomass of all boles ≥ 10 cm DBH) starting from the 32 inventories in Venezuela is critical. TAGB in the Venezuelan data can be presumed to have been estimated without bias, but the volume used in obtaining SB was apparently overestimated by assuming that the bole is a perfect solid of revolution. However, this will not create a bias in the estimate of TAGB at other sites (such as the inventories of RADAMBRASIL in Brazilian Amazonia) because the same volume overestimate occurs in these other inventories. BEF, based on correct TAGB and SB overestimated in the 32 plots in Venezuela, would compensate for similar errors in the estimate of SB in the RADAMBRASIL inventories. In other words, in determining the BEF any consistent bias in the value of SB is compensated for in the adjustment of the regression derived by Brown (equations 3 and 4). In the case of the 32 plots, Brown et al. (1989) obtained BEF = 1.74 (95% CI = 0.08) from the biomasses of the individual trees in the 32 plots as estimated using the allometric relationship for individual trees described in equation 6. Later, Brown and collaborators considered plots with lower TAGB and obtained equation 3 to estimate BEF starting from SB and TAGB. Therefore, there is no reason to expect bias in the estimate of commercial volume (or SB) in the plots studied by Brown and collaborators; since the volume (and therefore SB) of the boles inventoried was also overestimated by RADAMBRASIL, there will not be bias in the final estimate of TAGB when applied to the RADAMBRASIL data.

5. Conclusions

Irregularly shaped and hollow boles lead to significant errors in measurements of bole volume in central Amazonia. These errors result in an overestimate of 11.2% in the total bole volume per hectare. For RADAMBRASIL inventories, tree volume per hectare was overestimated by 4.4%. The additional effect of hollow trunks is only 0.7%. Both effects are greater in large trees, which tend to have more irregular boles and higher frequencies of hollow trunks. The effect of irregularities is related to the occurrence and distribution of tropical species that have boles with accentuated indentations. Tree hollows and irregularities are highly species-specific; therefore the data and conclusions in this study may not be representative of other tropical forests. The effect of these factors on stand biomass in each forest will depend on the abundance of species with accentuated irregularities. In spite of these errors being present in the stand volume tables of the RADAMBRASIL inventories, compensating errors in the formulas used to interpret volume data mean that there is no net bias in biomass calculations from such stand volume tables based on widely used equations (e.g., Brown et al., 1989; Brown and Lugo, 1992).

Acknowledgments

We thank the National Council for Scientific and Technological Development (CNPq AI470765/01-1) and the National Institute for Research in the Amazon (INPA PPI I-3620) for financial support. Three reviewers contributed valuable comments.

6. References

Adobe Systems, Inc. 1996. Adobe Photoshop. Version 4.0. Adobe Systems, Inc. San Diego, California, U.S.A.

Ahrens, S.; Holbert, D. 1981. Uma função de forma de tronco e volume de Pinus taeda L. Boletim de Pesquisa Florestal 3, 37-68.

Amelung, W.; Martius, C.; Bandeira, A. G.; Garcia, M. V. B.; Zech, W. 2002. Lignin characteristics and density fractions o termite nests in Amazonian rain forest – indicators of termite feeding guilds? Soil Biology & Biochemistry 34, 267-372.

Brazil, Projeto RADAMBRASIL. 1978. Folha SA.20, Levantamento de Recursos Naturais. Manaus. Vol. 18. Departamento Nacional de Produção Mineral, Rio de Janeiro, Brazil. 747 pp

Brown, I. F.; Martinelli, L. A.; Thomas, W.; Moreira, M. Z.; Ferreira, C. A.; Victoria, R. A. 1995. Uncertainty in the Biomass of Amazonian Forests: an Example from Rondônia, Brazil. Forest Ecology and Management 75, 175-189.

Brown, S. 1997. Estimating biomass and biomass change of tropical forest: A Primer. Forestry Paper 134, Food and Agriculture Organization of the United Nations (FAO), Rome, Italy. 55 pp.

Brown, S.; Gillespie, A. J. R.; Lugo, A. E. 1991. Biomass of tropical forests of South and Southeast Asia. Canadian Journal of Forest Research 21, 111-117.

Brown, S.; Gillespie, A. J. R.; Lugo, A. E. 1989. Biomass estimation methods for tropical forest with applications to forest inventory data. Forest Science 35(4):881-902.

Brown, S.; Lugo, A. 1992. Aboveground biomass estimates for tropical moist forest of the Brazilian Amazon. Interciencia 17(1), 8-18.

Castilho, C. V. 2004. Variação espacial e temporal da biomassa arbórea viva acima do solo em uma floresta de terra-firme na Amazônia central. Doctoral thesis in ecology, Instituto Nacional de Pesquisas da Amazônia/Fundação Universidade Federal do Amazonas, Manaus, Amazonas, Brazil. 72 pp.

Chave, J.; Riéra, B.; Dubois, M. A. 2001. Estimation of biomass in a neotropical forest of French Guiana: Spatial and temporal variability. Journal of Tropical Ecology 17:79-96.

Clark, D. B. 2002. Are tropical forests an important carbon sink? Reanalysis of the long-term plot data. Ecological Applications 12, 3-7.

Clark, D. B.; Clark, D. A. 2000. Landscape-scale variation in forest structure and biomass in a tropical rain forest. Forest Ecology and Management 137, 185-198.

do Nascimento, H. E. M. 2002. Biomassa Total Acima do Solo e a Fragmentação de Floresta de Terra-firme na Amazônia central. Doctoral thesis in ecology, Instituto Nacional de Pesquisas da Amazônia/Fundação Universidade Federal do Amazonas. Manaus, Amazonas, Brazil. 98 pp.

Fearnside, P. M. 1992. Forest biomass in Brazilian Amazônia: Comments on the estimate by Brown and Lugo. Interciencia 17(1), 19-27.

Fearnside, P. M. 1997a. Wood density for estimating forest biomass in Brazilian Amazonia: Forest Ecology and Management 90, 59-87.

Fearnside, P. M. 1997b. Greenhouse gases from deforestation in Brazilian Amazonia: net committed emissions. Climatic Change 35, 321-360.

Fearnside, P. M. 2000. Global warming and tropical land-use change: greenhouse gas emissions from biomass burning, decomposition and soils in forest conversion, shifting cultivation and secondary vegetation. Climatic Change 46, 115-158.

Fearnside, P. M.; Laurance, W. F. 2003. Comment on "Determination of deforestation rates of the world's humid tropical forests". Science 229, 1015a.

Fearnside, P. M.; Laurance, W. F. 2004. Commentary: Tropical deforestation and greenhouse-gas emissions. Ecological Applications 14(4), 982-986.

Fernandes, N. P.; Jardim, F. C. S.; Higuchi, N. 1983. Tabelas de volume para floresta tropical de terra-firme da Estação Experimental de Silvicultura Tropical do INPA. Acta Amazonica 13(3-4), 537-545.

Higuchi, N.; Ramm, W. 1985. Developing bole wood volume equations for a group of tree species of central Amazon (Brazil). Commonwealth Forestry Review 64(1), 33-41.

Houghton, R. A. 2003. Why are estimates of the terrestrial carbon balance so different? Global Change Biology 9, 500-509.

Houghton, R. A.; Lawrence, K. T.; Hackler, J. L.; Brown, S. 2001. The spatial distribution of forest biomass in the Brazilian Amazon: a comparison of estimates. Global Change Biology 7(7), 731-746.

INMET, 2003. Instituto Nacional de Meteorologia. www.inmet.gov.br. Accessed 12 Aug. 2003.

Magnago, H.; Barreto, R. A. A.; Pastore, U. 1978. Projeto RADAMBRASIL, Folha SA.20, Parte IV-Vegetação. Rio de Janeiro, Brazil. pp. 413-530.

Moura, J. B. 1994. Estudo da forma do fuste e comparação de métodos de estimativa volumétrica de espécies florestais da Amazônia brasileira. Masters Thesis, Universidade Federal do Paraná. Curitiba, Paraná, Brazil. 114 pp.

Putz, F. E.; Coley, P. D.; Lu, K.; Montalvo, A.; Aiello, A. 1983. Uprooting and snapping of trees: structural determinants and ecological consequences. Canadian Journal of Forestry Research 13, 1011-1020.

Ribeiro, R. J. 1996. Estudos de função de forma para espécies florestais de terra-firme da Amazônia. Masters dissertation in tropical forest science, Instituto Nacional de Pesquisas da Amazônia/Fundação Universidade do Amazonas, Manaus, Amazonas, Brazil. 76 pp.

Rodrigues, W. A.; Valle, R. C. 1964. Ocorrência de troncos ocos em mata de baixio da região de Manaus, Amazonas. Pub 16, Botânica, Instituto Nacional de Pesquisas da Amazônia, Manaus, Amazonas, Brazil. 8 pp.

Sheil, D. 1995. A critique of permanent plot methods and analysis with examples from Budongo Forest, Uganda. Forest Ecology and Management 77, 11-34.

Yamazaki, D. R.; Costa, A. M. R.; Azevedo, W. P. 1978. Projeto RADAMBRASIL, Folha SA.20, Parte III-Pedologia. Rio de Janeiro, Brazil. pp. 247-410.

FIGURE LEGENDS

Figure 1. Cross sections of boles of trees included in Table 2: A. Swartzia polyphylla DC. (Paracutaca); B. Chrysophyllum sanguinolentum (Pierre) Baehni ssp. spurium (Ducke) T. D. Penn. (Leitera), and C. Pouteria cladantha Sandwith (Abiurana).

Figure 2. A. Conventional DBH assuming a circular cross section is plotted against the corrected DBH, which is the diameter of a circle having the true area of the cross section determined from disk tracings. All but the six species with highly irregular boles shown in panel B are included. B. Irregular trees: (a) Astronium lecointei Ducke, (b) Minquartia guianensis Aubl., (c) Aspidosperma discolor A. DC., (d) Aspidosperma discolor A. DC., (e) Swartzia polyphylla DC., and (f) Chimarris turbinata DC.

Figure 3. Conventional versus corrected DBH for large trees (DBH ≥ 40 cm; n = 52). One tree was excluded for which the correction was approximately -400%. Circle symbols represent the section at breast height (1.36 m) and “x” symbols represent the section at the end of the bole. The plot shows clearly that the magnitude of the correction increases at larger tree diameters and that the relationship has high variability.

Figure 4. Estimated volume of the bole decreases when the corrected DBH is used. The correction and the variance of the correction are both greater for larger trees. Paired symbols for each tree show the effect of correcting only for cross section shape (open circles) and the effect of correcting for both shape and hollows (x symbols).

Figure 5. Frequency of hollow trees by diameter class.

Table 1. Number of trees sampled by size class and replication factors to emulate known stem density in central Amazonia.

Conventional DBH	Number of trees sampled	Replication factor*	Stems/ha
≥5 - <10	36	19.8	714
≥10 - <15	45	5.6	253
≥15 - <20	52	2.6	136
≥20 - <25	41	1.9	77
≥25 - <30	37	1.3	47
≥30 - <35	27	1.1	30
≥35 - <40	15	1.5	22
≥40 - <45	17	1.0	17
≥45 - <50	13	1.0	13
≥50 - <55	3	2.0	6
≥55 - <60	6	1.0	6
≥60 - <65	3	1.0	3
≥65 - <70	2	1.0	2
≥70 - <75	1	1.0	1
≥75 - <80	1	1.0	1
≥80 - <85	0	-	0
≥85 - <90	2	1.0	2
≥90 - <95	1	1.0	1
≥95 - <100	0	-	0
≥100 - <105	0	-	0
≥105	1	1.0	1
Total	303	-	1332

* Replication factors are multipliers for weighting the number of trees sampled in each DBH class by the frequency of that class in Central Amazonian forests (i.e., the quotient of “stems/ha” divided by “number of trees sampled”).

Species:	A. *Swartzia polyphylla* DC. (Paracutaca);	B. *Chrysophyllum sanguinolentum* (Pierre) *Baehni* ssp. *spurium* (Ducke) T. D. Penn. (Leitera)	C. *Pouteria cladantha* Sandwith (Abiurana)
(1) Conventional area (cm²)	5865.8	319.9	630.3
(2) Corrected area (cm²)	1133.1	252.0	555.9
Overestimate (%)	417.7	26.9	13.4

Euler Melo Nogueiraa; Bruce Walker Nelsonb, Philip M. Fearnsideb*

2.2. Evaluation of circumference measures for obtaining the volume of the bole.

3.1. Effect of non-circular form and of hollows on conventional estimates of diameter, basal area and wood volume

VEF = 1.25 for dense forests and 1.5 for other Amazonian forests;

WD = 0.69 g cm-3;

BEF = exp{3.213 - 0.506 Ln SB}, for SB < 190 Mg ha-1;

BEF = 1.74, for SB > 190 Mg ha-1;

SB = Stand biomass (biomass of boles ≥ 10 cm DBH) = Inventoried volume × VEF × WD

6. References

Euler Melo Nogueira^a; Bruce Walker Nelson^b, Philip M. Fearnside^b*

WD = 0.69 g cm^-3;

BEF = exp{3.213 - 0.506 Ln SB}, for SB < 190 Mg ha^-1;

BEF = 1.74, for SB > 190 Mg ha^-1;